Now, by construction, each half of this triangle is a triangle Q What observations can you make about the relationship between the trigonometric ratios of 30 degrees and 60 degrees?Here is the proof that in a 30°60°90°30 degrees 60 degrees 90 degrees Yes they do, all measurements are the same The 90 degrees in one corner of the triangle (bottom), the 30 degrees belongs on the top corner and the 60 degrees belongs on the right hand corner A special triangle is called an Equilateral Triangle (all sides are the same length)
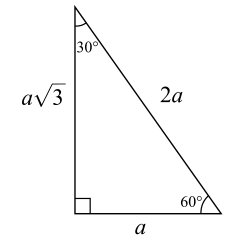
The Shorter Leg Of A 30 60 90 Right Triangle Is 7 5 Inches How Long Is The Longer Leg And The Hypotenuse Socratic
Trigonometry 30 60 90 degree triangle
Trigonometry 30 60 90 degree triangle-30 60 90 Triangle Ratio A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherYou will frequently need to know the values of sine, cosine and tangent for the angles listed above What follows will try to cut down on the amount of memorization and also explain where the values come from
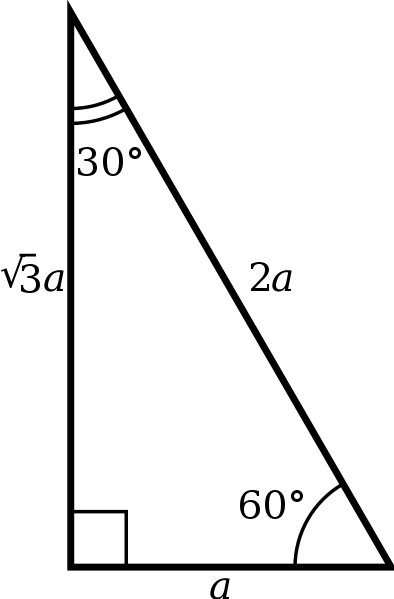



30 60 90 Triangle Formulas Rules And Sides Science Trends
Special Right Triangles 30°60°90°Honors Math Il Unit 5 Right Triangles Name Pyþhagorean Theorem Intro to Trig SOH CAH TOA Using trig to find the Missing Side Using Trig to Find the Missing Angle , Triangles Angles of Elevation and Depression and Word Problems pg 1 Points 10Check out this tutorial to learn about triangles!
One of the two special right triangles you'll be facing in trigonometry is the triangle The other one is the 45 45 90 triangle These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems(π / 6), 60°This is a triangle whose three angles are in the ratio 1 2 3 and respectively measure 30°
A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using theA 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three This special type of right triangle is similar to the 45 45 90 triangleFollow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides




The Shorter Leg Of A 30 60 90 Right Triangle Is 7 5 Inches How Long Is The Longer Leg And The Hypotenuse Socratic




30 60 90 Triangle Theorem Ratio Formula Video
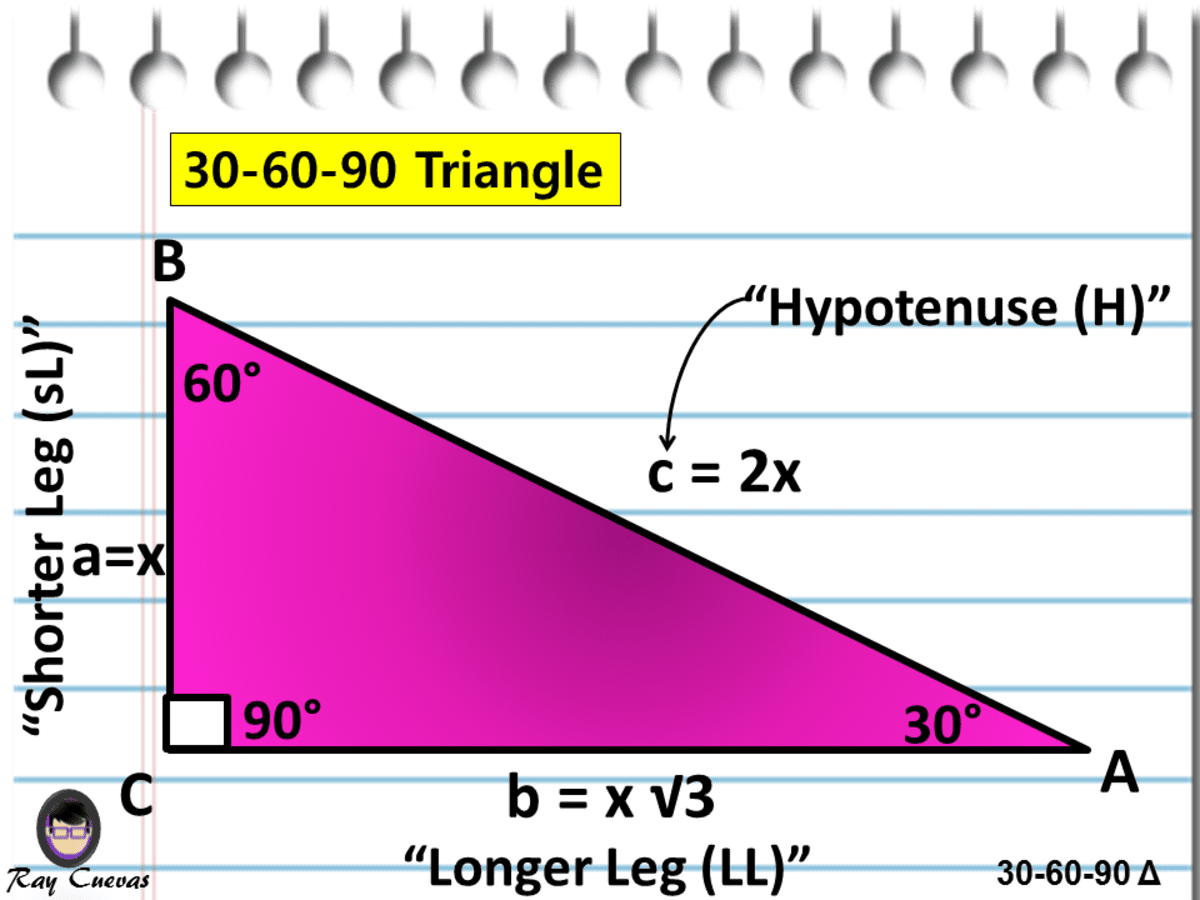
(Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30°We know that in a 3060=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10 The formula for , so orSince the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a 2 b 2
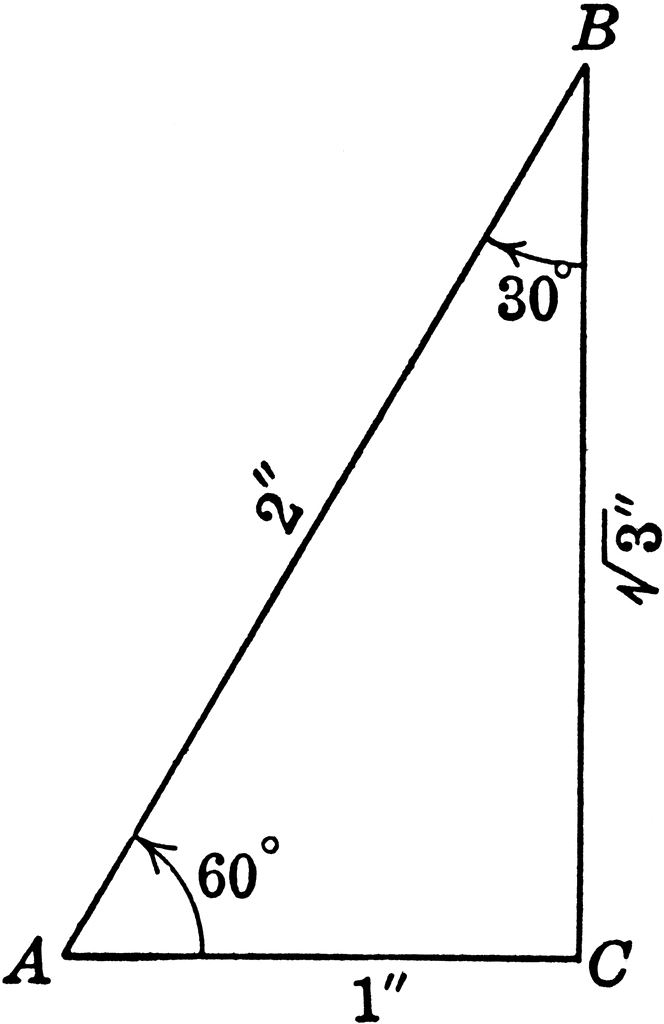



Special Right Triangle With Angles 30 60 90 Degrees Clipart Etc



The Easy Guide To The 30 60 90 Triangle
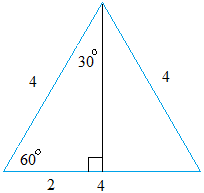
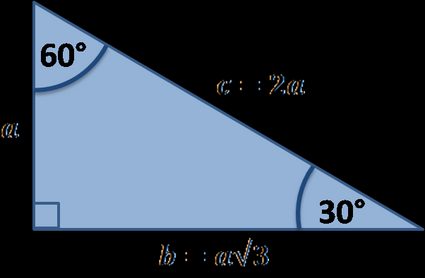
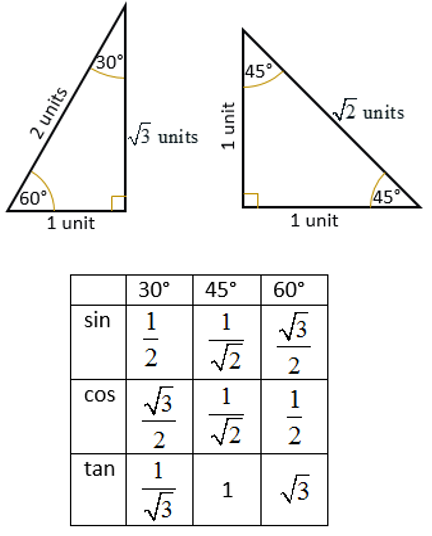
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!The trigonometric ratios for 30^o, 45^o, and 60^o are based on some standard triangles sin, cos, and tan (and their reciprocals) are the ratios of the sides of these triangles Both 30^o and 60^o are based on an equilateral triangle with sides of length 2 and with one of the angles bisected The 45^o angle is based on an isosceles triangle with the equal sides having a19 $149 PDF This worksheet is only over special right triangles I have 2 example problems at the top of the page One example is for if given the hypotenuse, find the missing legs The other example is for if given the side (x sq rt 3), find the short leg (x) and the hypotenuse (2x) There are a total
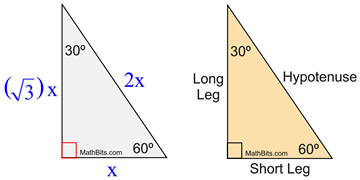



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Using The 30 60 90 Triangle To Find Sine And Cosine
A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!9 5 Trigonometric Ratios Geometry Objectivesassignment Find The Trigonometric Ratios Of Some Specific Angles Special Right Triangles Fully Explained W 19 Examples Trig Values For Paper 1 Triangle Method Gcse 30 60 90 Triangles Special Right Triangle Trigonometry Youtube 30 60 90 Triangles Special Right Triangle Trigonometry Youtube(π / 3), and 90°




Special Triangles Used In Trigonometry




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
In the study of trigonometry, the triangle is considered a special triangle Knowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30°13 Trig values for 0°, 30°,45°,60°, and 90°Triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90°



3




Learn How To Evaluate The Six Trig Functions Of A 30 60 90 Triangle Youtube
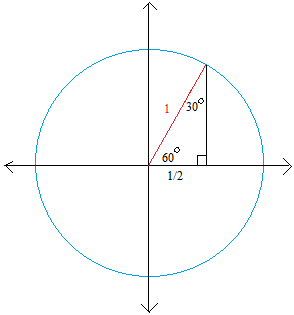
(π / 2)The sides are in the ratio 1 √ 3 2 The proof of this fact is clear using trigonometryThe geometric proof is Draw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BCA right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32Angles, it will also be a perpendicular bisector to its opposite side




30 60 90 Triangle Formulas Rules And Sides Science Trends



1
Draw an equilateral triangle all sides are equal and the angles are all 60 deg From any angle drop a line perpendicular to the base(an altitude) By triangle congruence laws you can prove the 2 resulting triangles are congruent which means the alIn Example 2 of Section 12, we saw that in a right triangle, the ratio of the shortest side to the hypotenuse was \(\frac{1}{2}\text{,}\) or 05This ratio is the same for any two right triangles with a \(30\degree\) angle, because they are similar triangles, as shown at rightThe type of trig function in order to find the angle measure when given two sides of a right triangle Long Leg The side of a triangle which equals the Short leg x sq rt 3



13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
2 The triangle Begin with an isosceles right triangle (construct a segment, rotate it 90 degrees, connect the two remaining verticesRefers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90°Triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60°




Special Right Triangle Wikipedia




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Get Free 30 60 90 Triangle Answers Algebra 2 A Quick Guide to the Degree Triangle dummies The correct answer is Choice (A) If one of the angles is 30 degrees, the other angle is 60 degrees, making this a triangle, with a side ratio of The 2 is the hypotenuse, making the other Page 14/42A proof that sin(30) = 1/2, cos(30) = √3/2, sin(60) √3/2, cos(60) = 1/2 is as follows Consider an equilateral triangle, all angles are 60ºDrop a bisector from one of the 60º




30 60 90 And 45 45 90 Triangles Youtube




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherIntro to Trig be 60 degrees And the lesser of those two angles is half of what was an angle of the original triangle, so its measure must be 30 degrees Now we've got what we need to find the sine, cosine, and tangent of 30 degrees and 60 degrees Using righttriangle trig definitions, you




Trig Ratios Of Special Triangles Article Khan Academy



How To Find Sine And Cosine Using The Unit Circle



45 45 90 And 30 60 90 Triangles Zona Land Education




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Explanation Examples




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Right Triangle Side Ratios Expii



3
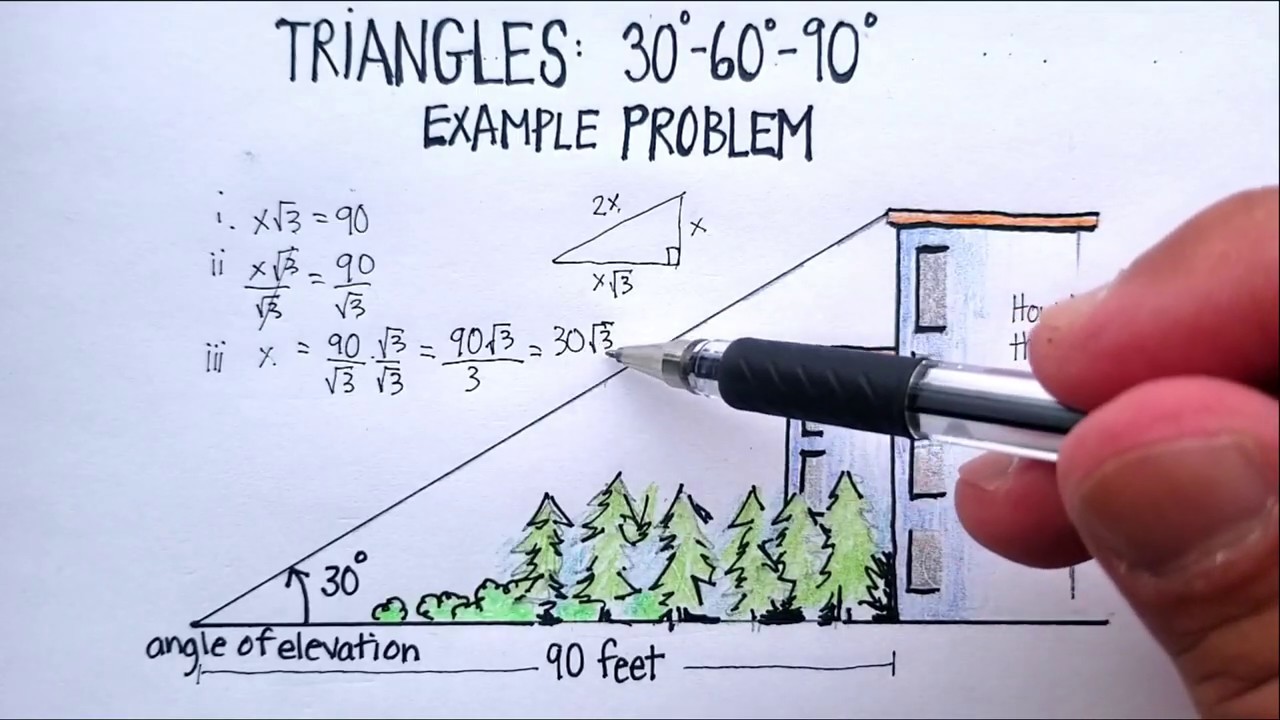



Triangles Special Right Triangles 30 60 90 Example Problem Youtube




This Set Includes 4 Posters On Trigonometric Ratios Common Trigonometric Ratios Sine Cosine Tangent Of 30 45 And 6 Teaching Math Math Resources Math Notes




The 30 60 90 Triangle Topics In Trigonometry




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangles Free Math Help
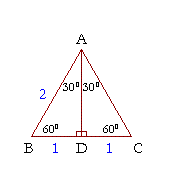



The 30 60 90 Triangle Topics In Trigonometry
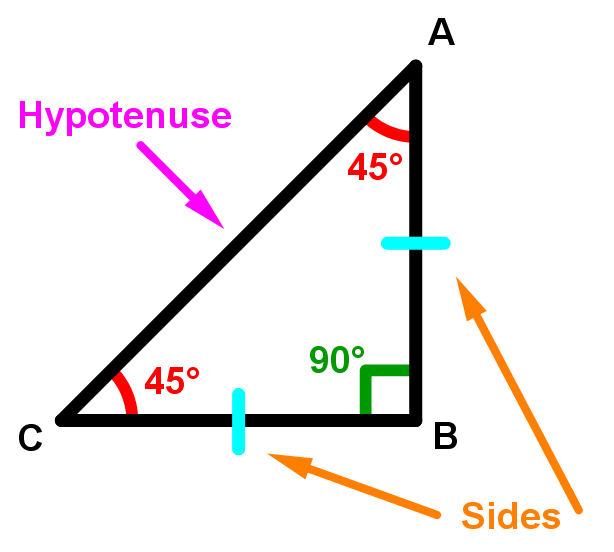



How To Use The Special Right Triangle 45 45 90 Studypug




Special Right Triangles Fully Explained W 19 Examples
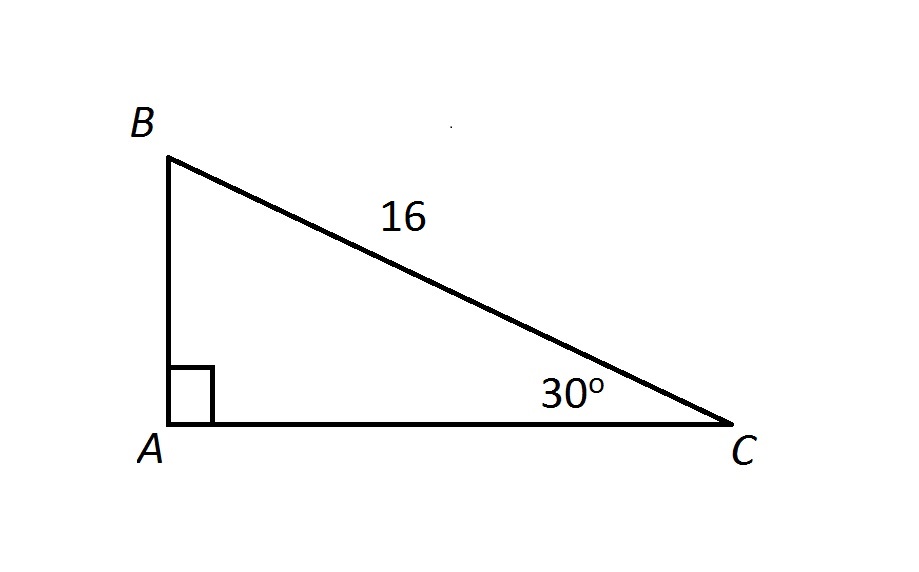



Special Triangles Hiset Math




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




30 60 90 Triangle Example Problem Video Khan Academy




The 30 60 90 Triangle Topics In Trigonometry




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangles Concept Trigonometry Video By Brightstorm
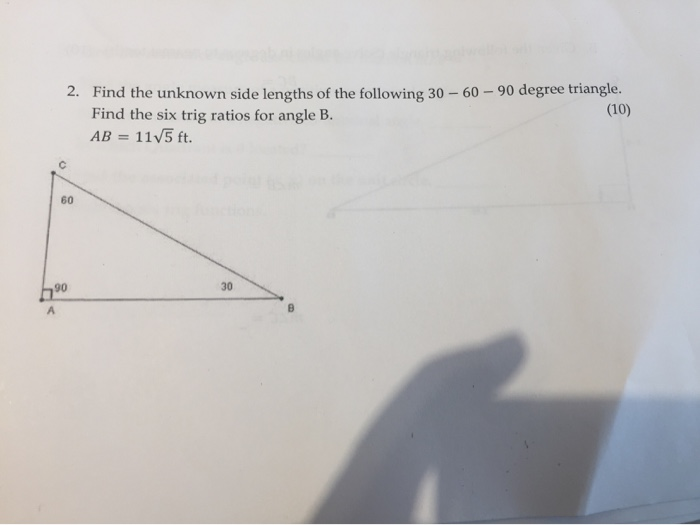



Solved 2 Find The Unknown Side Lengths Of The Following 30 Chegg Com



What Is The Best Way To Remember Evaluate The Trig Function Degree Values Using A Right Triangle Unit Circle Quora




Solved Trigonometry Prerequisite Special Right Triangles Chegg Com




30 60 90 Triangle Theorem Ratio Formula Video




A Quick Guide To The 30 60 90 Degree Triangle Dummies
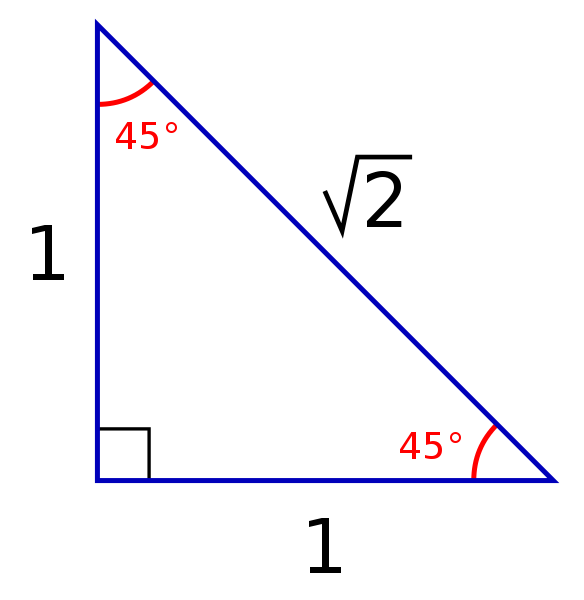



30 60 90 Triangle Formulas Rules And Sides Science Trends




The Complete Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
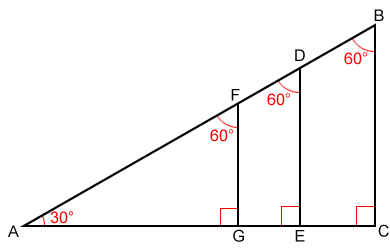



30 60 90 Triangle




Special Right Triangles Gmatsyllabus Com



1
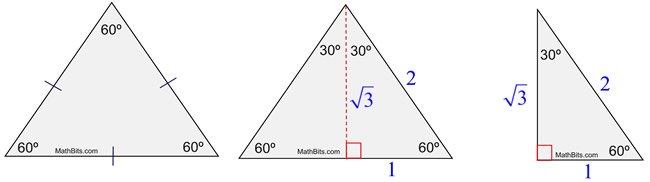



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangles
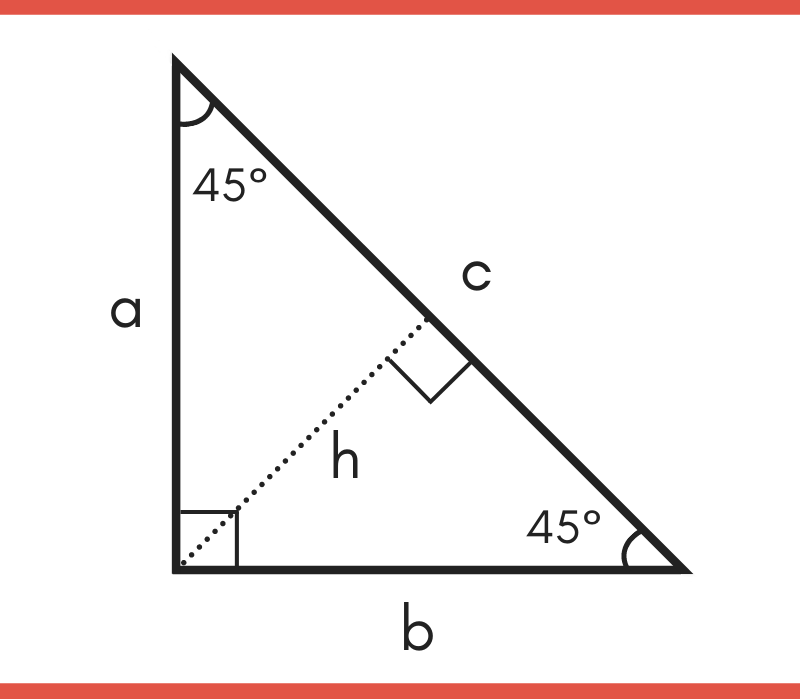



45 45 90 Special Right Triangle Calculator Inch Calculator
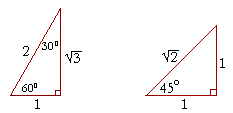



The 30 60 90 Triangle Topics In Trigonometry
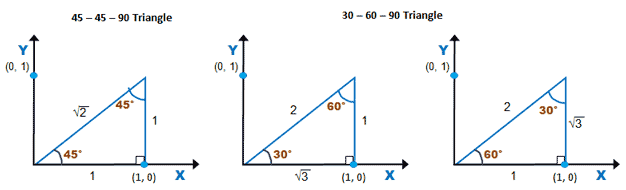



Trigonometry Snow Mountain




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Right Triangles Ck 12 Foundation
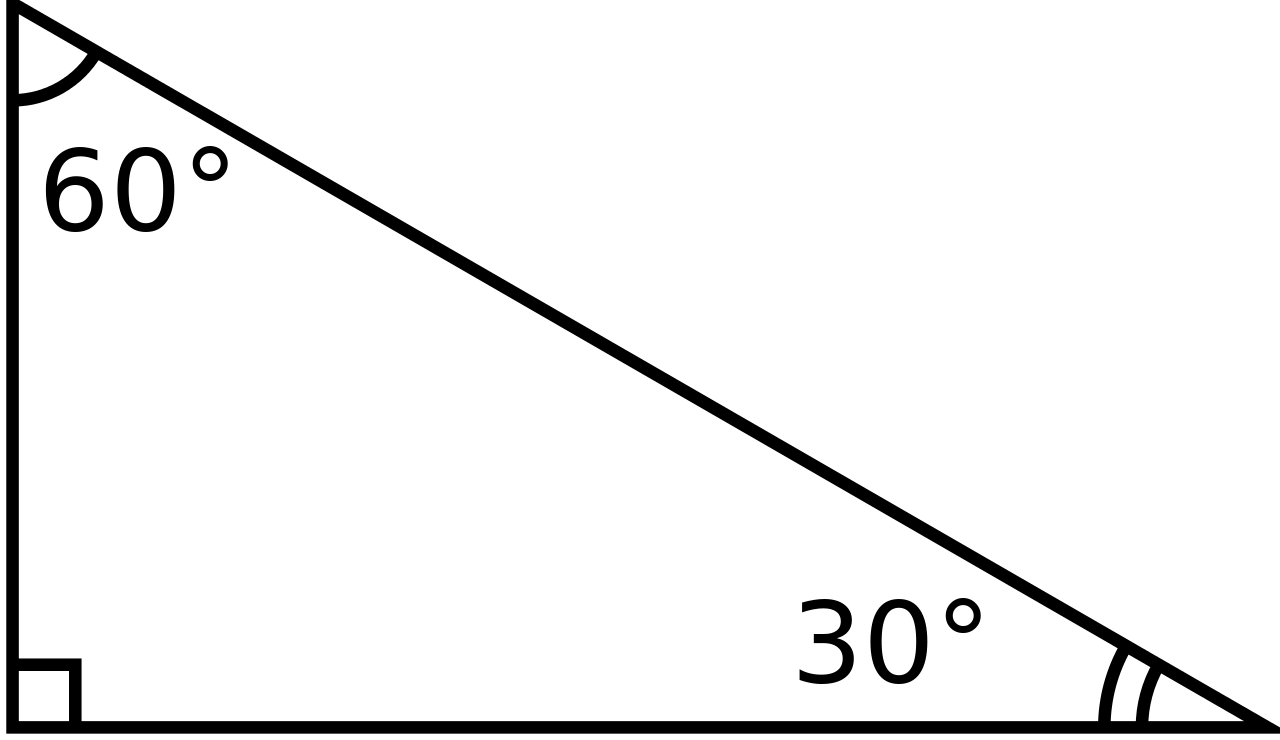



File 30 60 90 Triangle 2 Svg Wikimedia Commons



Unit Circle Trigonometry Learning Objective S Understand Unit Circle Reference Angle Terminal Side Standard Position Find The Exact Trigonometric Function Values For Angles That Measure 30 45 And 60 Using The Unit Circle Find The Exact




How To Work With 30 60 90 Degree Triangles Education Is Around
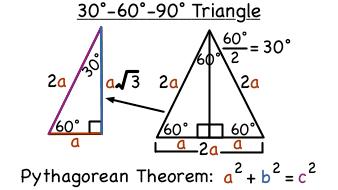



What Is A 30 60 90 Degree Triangle Virtual Nerd




Special Right Triangles Review Article Khan Academy




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




Trigonometry Act Math
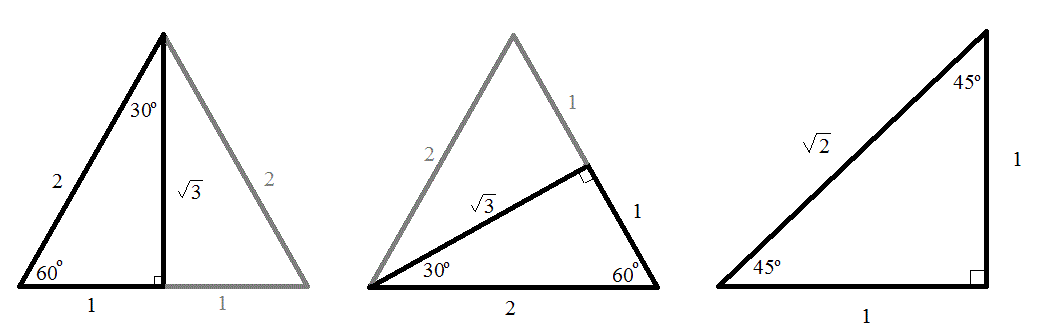



How Do You Find Trigonometric Ratios Of 30 45 And 60 Degrees Socratic




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




30 60 90 Triangle Definition Theorem Formula Examples



Right Triangle Trigonometry



30 60 90 Triangle Calculator Formula Rules




Ppt 30 60 90 Right Triangles Powerpoint Presentation Free Download Id




Special Right Triangles Use As An Extension To Conventional Pythagorean Theirem Right Triangle Gre Math Geometry Lessons



What Are The Six Trigonometric Functions For Angle 30 Using A 30 60 90 Triangle Quora



Trigonometric Ratios Of Special Angles 0 30 45 60 90 Video Lessons Examples And Solutions




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Special Right Triangle Calculator Inch Calculator



Special Right Triangle 30 60 45 45 37 53 Elearning
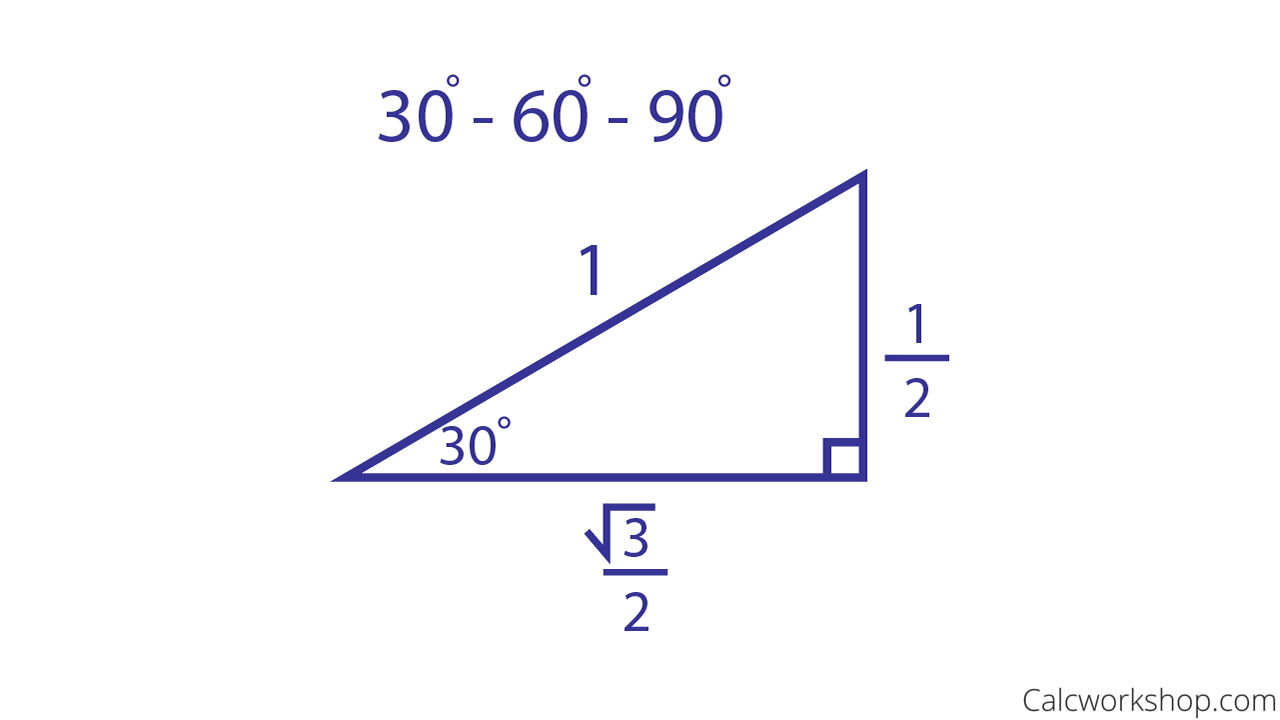



Unit Circle W Everything Charts Worksheets 35 Examples
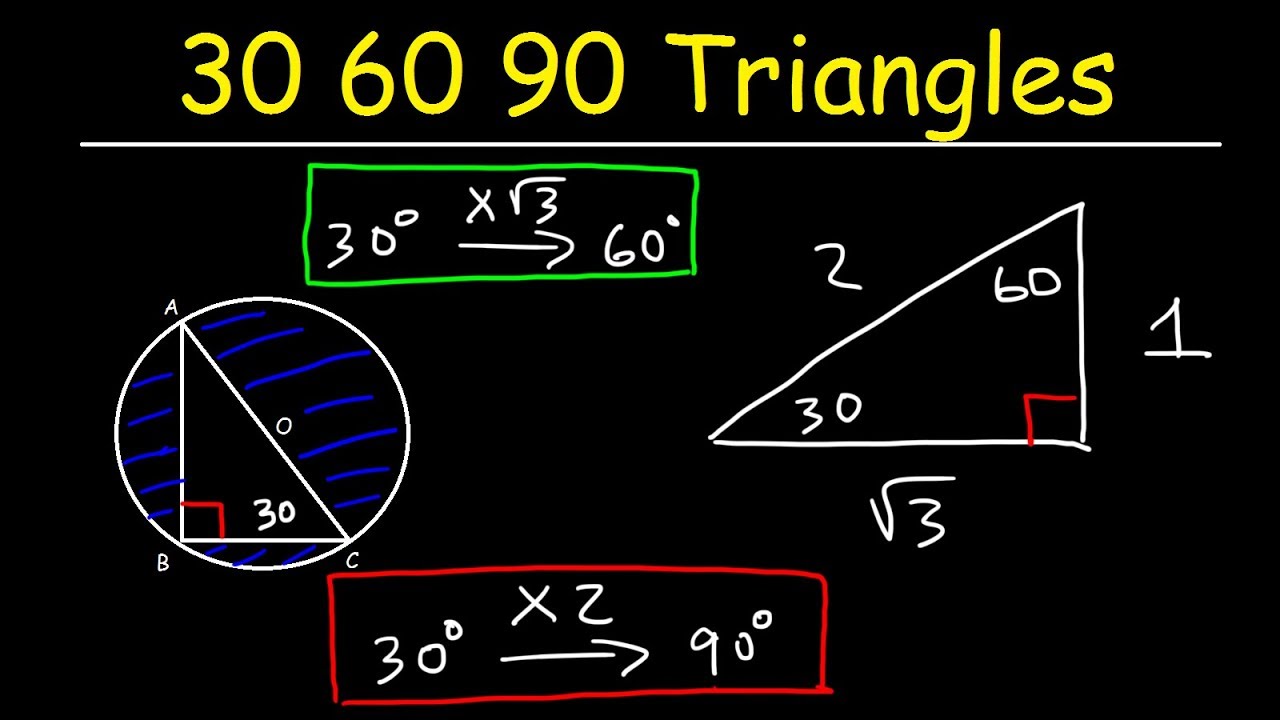



30 60 90 Special Right Triangles For Act Sat Math Geometry Trigonometry Youtube



A 30 60 90 Triangle



Precalculus Notes Trig 3
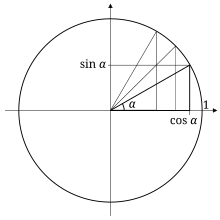



Special Right Triangle Wikipedia
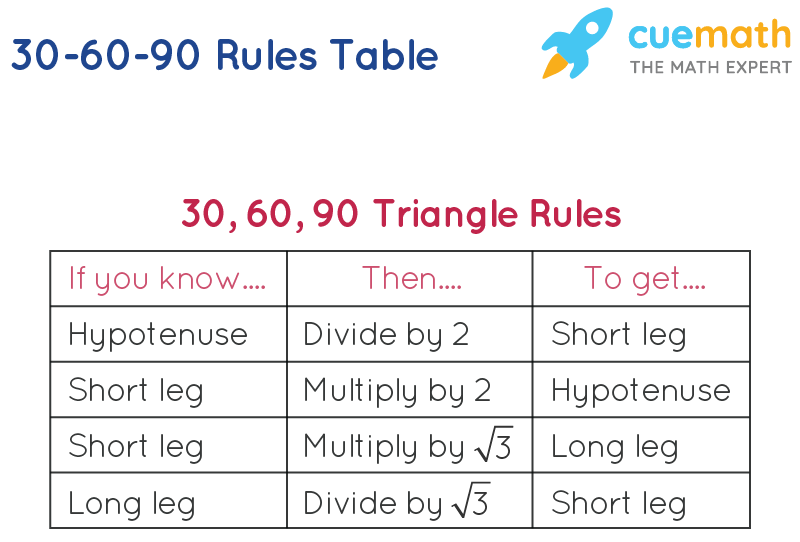



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Math Methods Studying Math Physics And Mathematics




30 60 90 Triangle Explanation Examples



Right Triangles Gmat Free
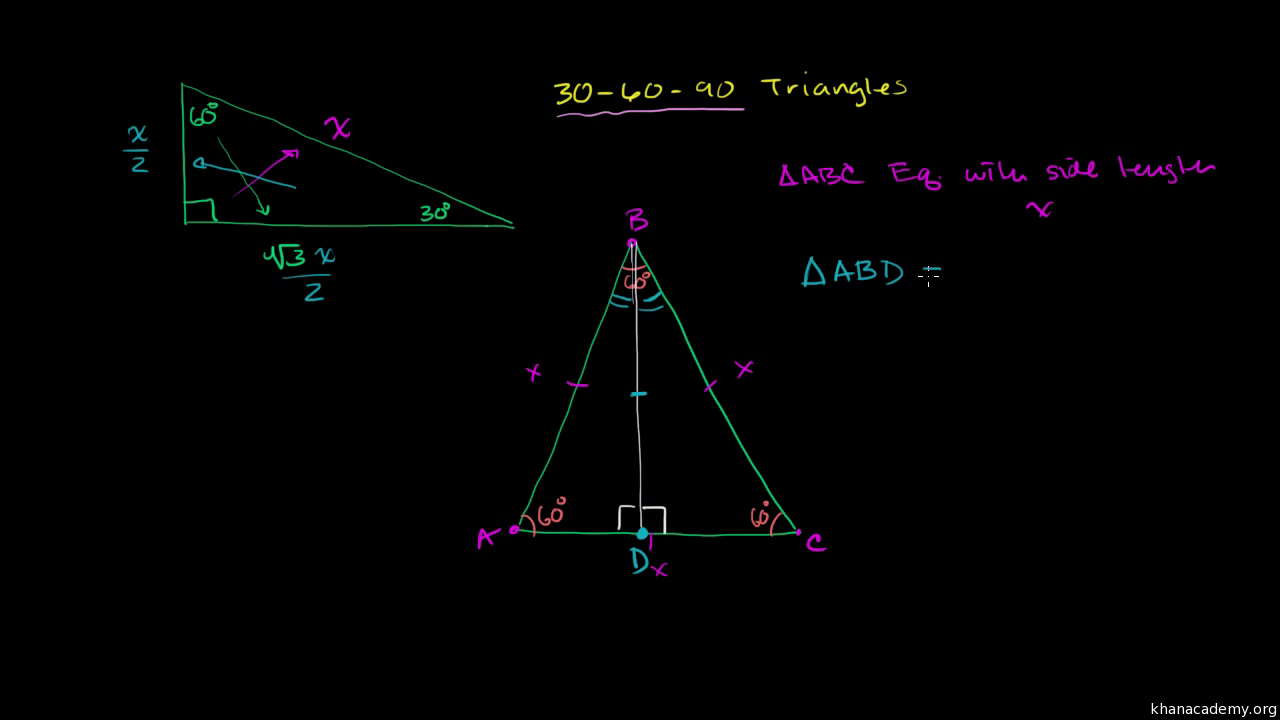



Special Right Triangles Proof Part 1 Video Khan Academy
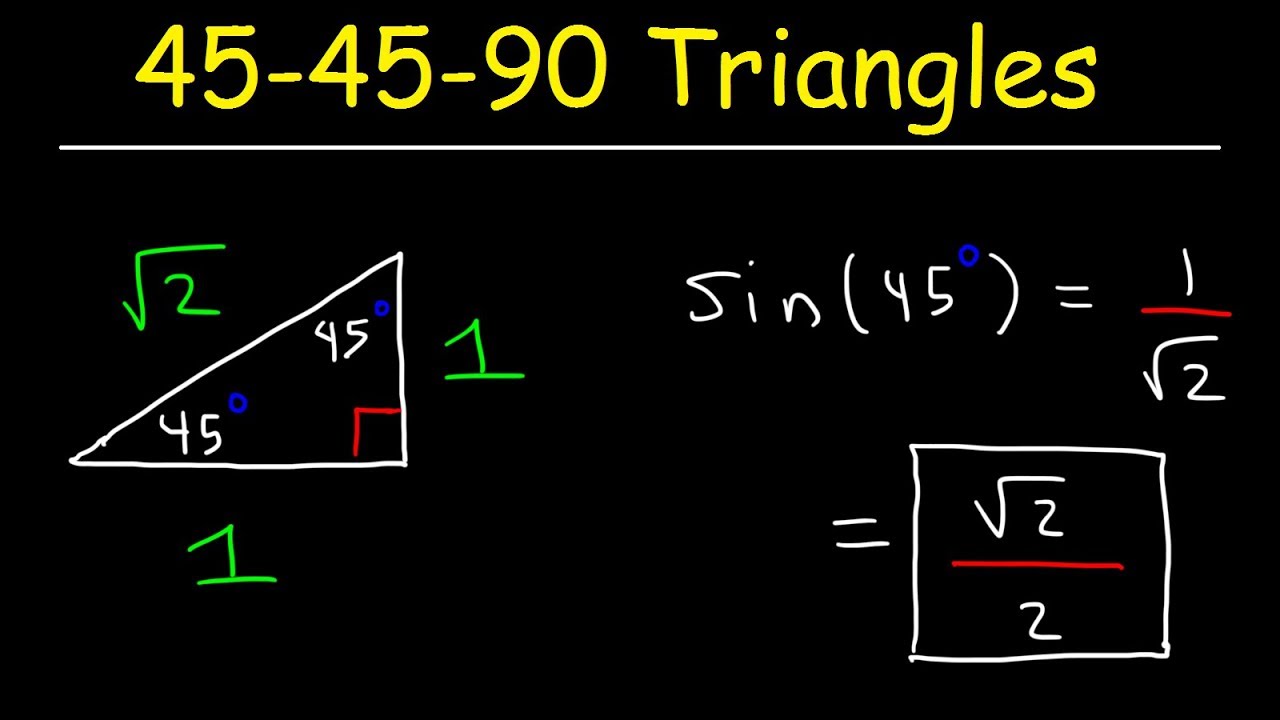



30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Triangle Calculator Formula Rules
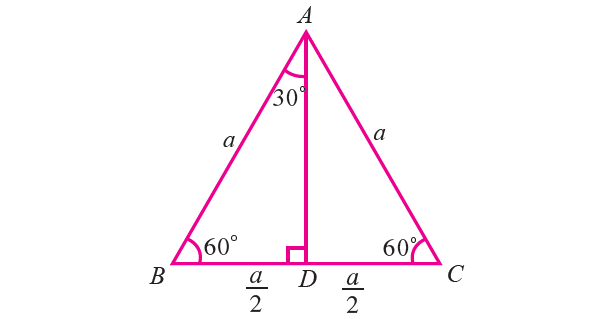



Trigonometric Ratio Table



Precalculus Notes Trig 3




Solved Trigonometry Prerequisite Special Right Triangles Chegg Com




30 60 90 Triangle Calculator Formula Rules
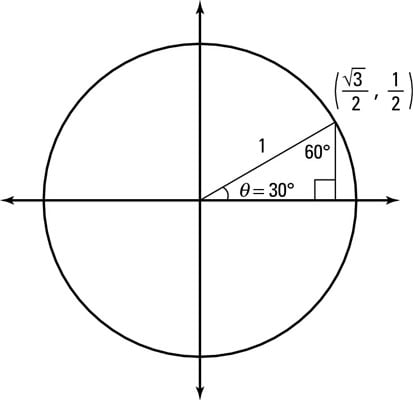



How To Plot The Major Angles Of The Whole Unit Circle Dummies



The Easy Guide To The 30 60 90 Triangle
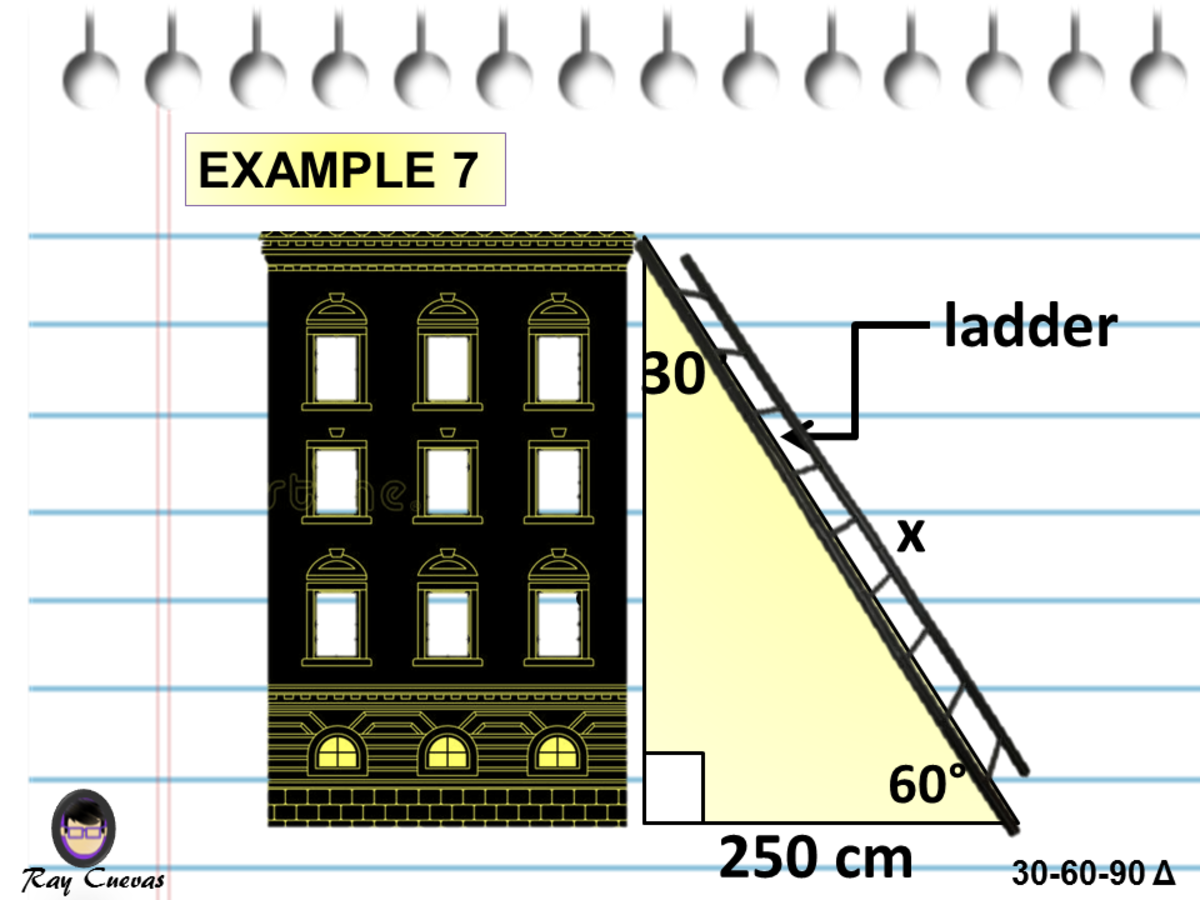



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Review Article Khan Academy
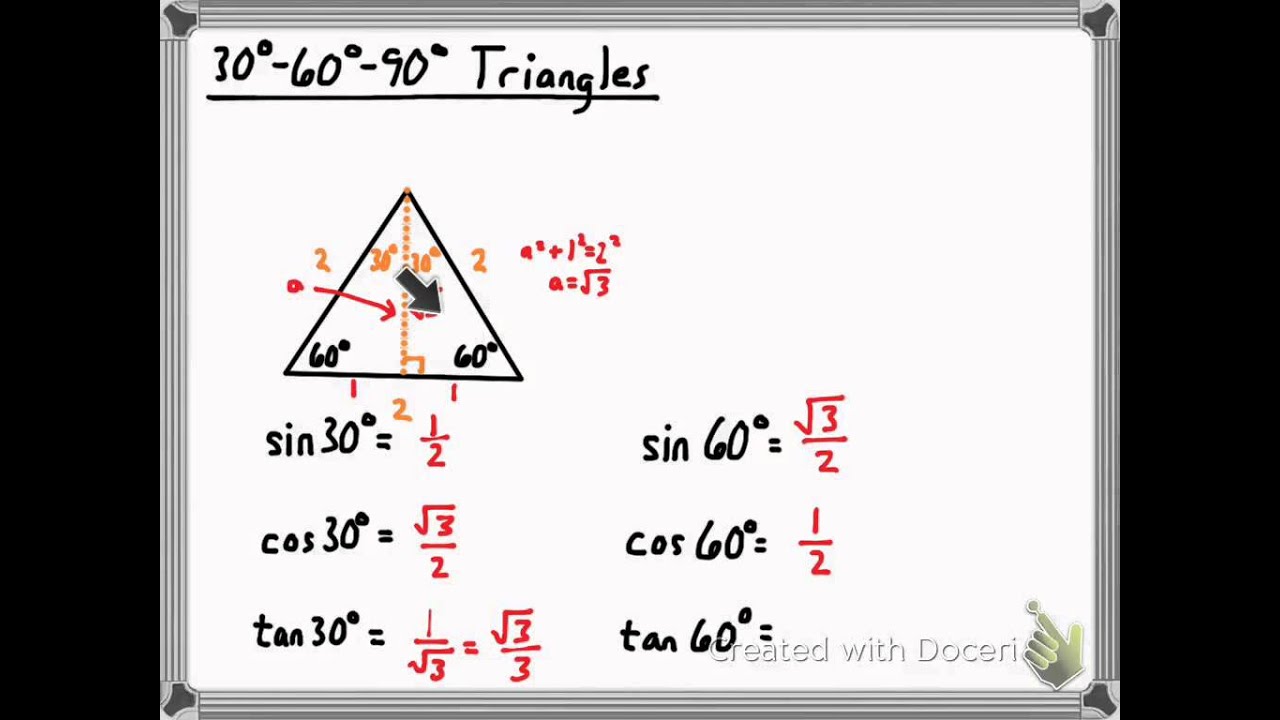



Trig Ratios For 30 60 90 Triangles Youtube




How To Use The Special Right Triangle 30 60 90 Studypug




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



0 件のコメント:
コメントを投稿