248 ELLIPSES Example Graph the ellipse 4x2 9y2 16x18y11 = 0 What are the center, vertices, and foci?To graph an ellipse, visit the ellipse graphing calculator (choose the "Implicit" option) Enter the information you have and skip unknown values Enter the equation of an ellipse In any form you want `x^24y^2=1`, `x^2/9y^2/16=1`, etc Enter the center ( , ) Enter the first focus ( , ) Enter the second focusFollow 36 views (last 30 days) Show older comments Emil Goh on Vote 0 ⋮ Vote 0 Commented Emil Goh on Accepted Answer Joseph Cheng new to matlap

Identifying Linear Functions Warm Up Lesson Presentation Lesson
Graph (x-4)^2/4+y^2/9=1 brainly
Graph (x-4)^2/4+y^2/9=1 brainly-(NOTE It can be shown using polar coordinates that the slope of the graph as it passes through the origin (twice !) is 1 and 1 Returning to (**), we next have that 1 x 2y 2 = 0 , or y 2 = 1 x 2 Substitute this into the original equation (x 2 y 2) 2 = 2x 22y 2, getting ( x 2 (1 x 2) ) 2 = 2x 22(1 x 2) , 1 = 2x 2 2 2 x 2, 3Textbook solution for Calculus Early Transcendental Functions 7th Edition Ron Larson Chapter 101 Problem 6E We have stepbystep solutions for your textbooks written by Bartleby experts!



Green Globs And Graphing Equations Buffalo State College Flip Ebook Pages 1 6 Anyflip Anyflip
X 2 4 y2 9 z 16 = 1 1Its graph is shown in Figure 123 2We illustrate –nding its traces by –nding the intersection of the ellipsoid with the xyplane, the plane z= 2, and the plane z= 8 Note that the last two planes are parallel to the xyplane Intersection with the xyplane On the xyplane, z= 0 hence the equation of the 73 The conjugate of the hyperbola x 2 a 2 − y 2 b 2 = 1 is x 2 a 2 − y 2 b 2 = − 1 Show that 5 y 2 − x 2 25 = 0 is the conjugate of x 2 − 5 y 2 25 = 0 74 The eccentricity e of a hyperbola is the ratio c a, where c is the distance of a focus from the center and a is the distance of a vertex from the centerName equation of trace in xzplane ;
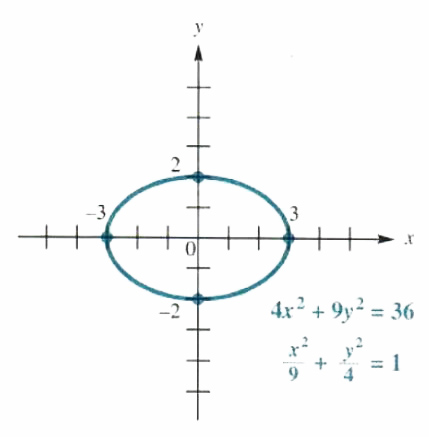
Graph the ellipse and its foci x^2/9 y^2/4=1 standard forms of ellipse (xh)^2/a^2 (yk)^2/b^2=1 (horizontal major axis),a>b (yk)^2/a^2 (xh)^2/b^2=1 (vertical major axis),a>b given ellipse has horizontal major axis center (0,0) x 2 /4 y 2 /9 = 1 The equation is y 2 /9 x 2 /4 = 1 The standard form of the equation of an ellipse center (h, k) with major and minor axes of lengths 2 2 (y k ) 2 /b 2 = 1 or (x h) 2 /b 2 (y k) 2 /a 2 = 1The vertices and foci lie on the major axis, a and c units, respectively, from the center (h, k ) and the relation between a, bRelated » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes
Midpoint ( − 4, − 2) 5 Distance √ 7 units;I)Given the equation (x^2)/4 (y^2)/9 = 1 (z^2) Find the traces parallel to the yzplane, that is, set x = k (a) Do we have to put a restriction on the value of k?Dx = " x5 15 − x8 24 # 2 0 = 32 15 − 256 24 = − 128 15 07 Example Evaluate Z π π/2




Ex 8 1 4 Find Area Bounded By Ellipse X2 16 Y2 9 1
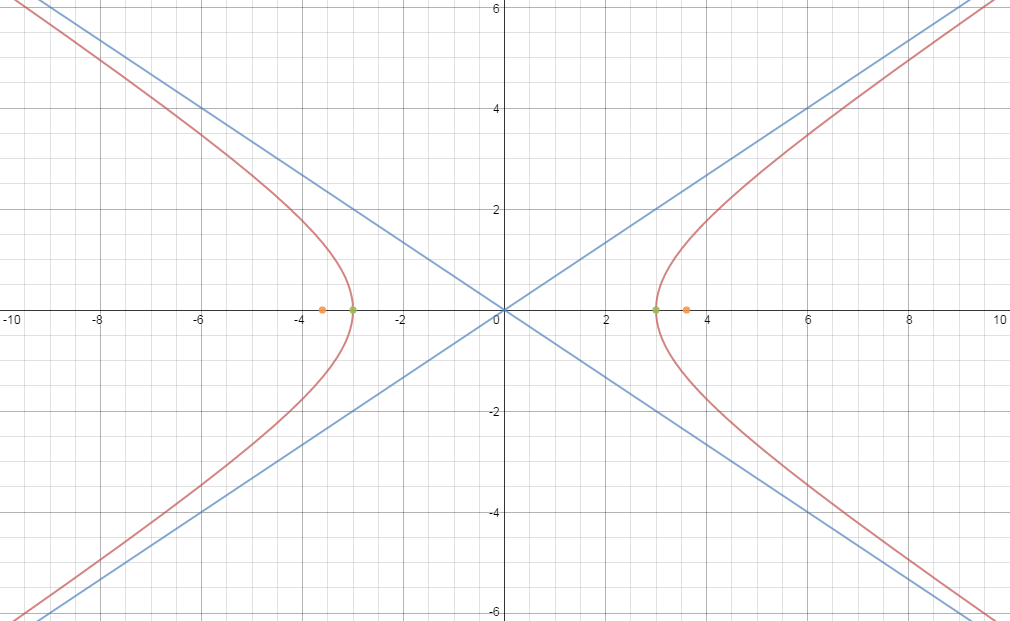



How Do You Find All The Critical Points To Graph 4x 2 9y 2 36 Including Vertices Foci And Asymptotes Socratic
X 2 4 − y 2 9 = 1 y 2 9 For the following exercises, assume an object enters our solar system and we want to graph its path on a coordinate system with the sun at the origin and the xaxis as the axis of symmetry for the object's path Give the equation of the flight path of each object using the given information(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;Y' x 2 4 y 3 = 2 2x y, and (Equation 1) Thus, the slope of the graph (the slope of the line tangent to the graph) at (1, 1) is Since y'= 4/5 , the slope of the graph is 4/5 and the graph is increasing at the point (1, 1) Now determine the concavity of the graph at (1, 1) Differentiate Equation 1, getting
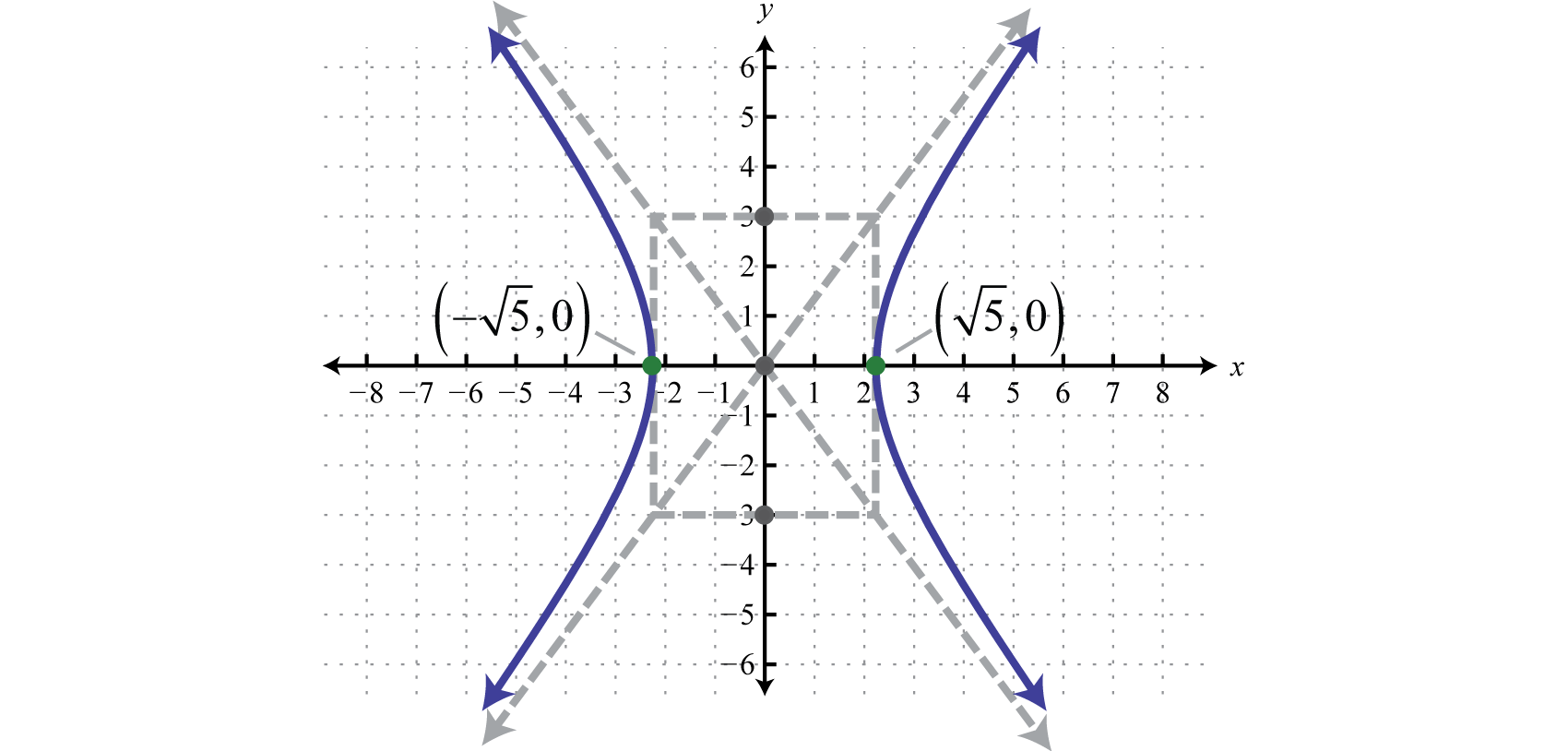



Hyperbolas
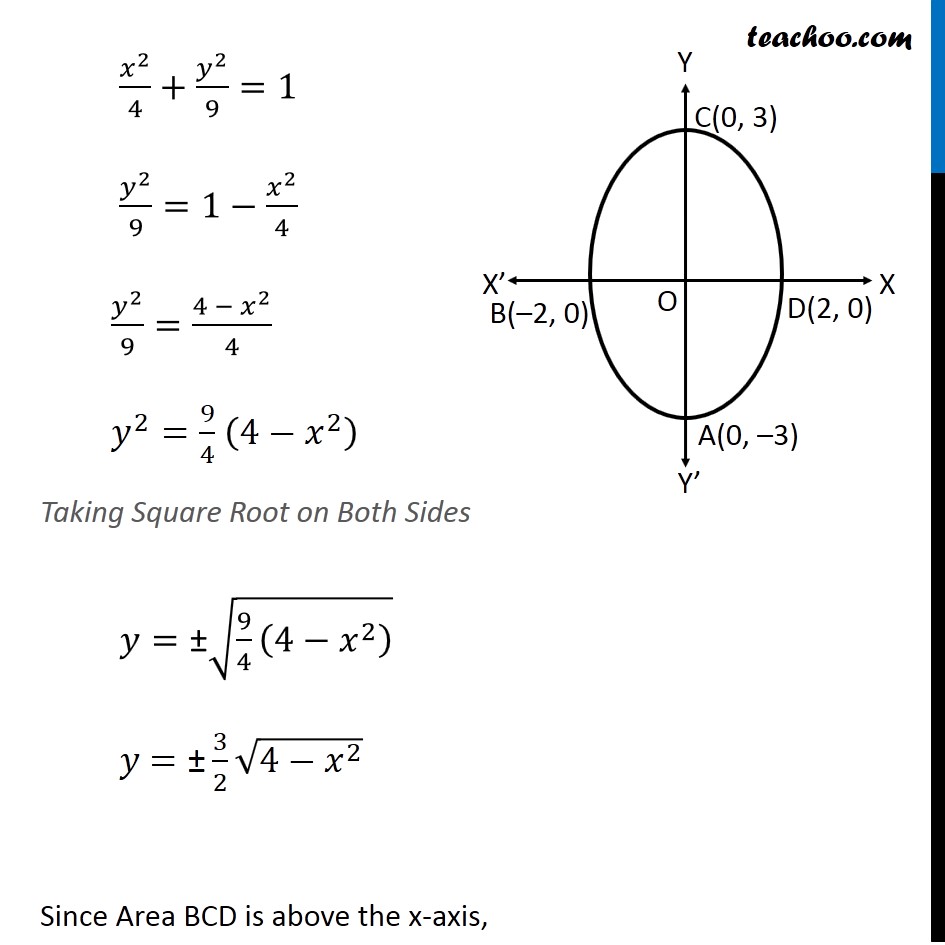



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12
Determine the type of conic section represented by the equation and graph it x 2 = 4 y – 8 ( x – 0 ) 2 = 4 ( y – 2 ) y – 2 = 1 ⁄ 4 ( x – 0 ) 2 The graph of this equation is a parabola The vertex is at ( 0, 2 ) The vertical axis is x = 0, which is the yaxisThis calculator will find either the equation of the hyperbola (standard form) from the given parameters or the center, vertices, covertices, foci, asymptotes, focal parameter, eccentricity, linear eccentricity, latus rectum, length of the latus rectum, directrices, (semi)major axis length, (semi)minor axis length, xintercepts, and yintercepts of the entered hyperbolaTranscribed Image Textfrom this Question For the surface x^2/4y^2/9z^2/16 = 1 , give the equations and names of the 2D traces, then name the 3D surface and sketch a graph equation of trace in xyplane ;



What Does X 4 2 4 Y 7 2 9 1 Represent Socratic



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
0 votes 1 answer Using integration, find the area of the region bounded by the parabola y^2 = 4x and the circle 4x^2 4y^2 = 9In this example the parametric equations are x = 2t and y = t 2 and we have evaluated t at −2, −15, −1, −05, −025, 0, 025, 05, 15 and 2 We have determined the corresponding values of x and y and plotted these points The diagram shows the result of plotting these pointsAnswer to Find the equations of both tangent lines to the graph of the ellipse {x^2} / 4 {y^2} / 9 = 1 that passes through the point (0, 4) not



Hyperbola Y 2 16 X 2 4 1 Youtube



X 4 2 9 Y 2 2 4 1 For The Ellipse Find The Center Foci And Vertices Graph The Equation Youtube
All of the following graphs have the same size and shape as the above curve I am just moving that curve around to show you how it works Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be movedIf so, what is the necessary restriction? 8E Conic Sections (Exercises) Calculate the distance and midpoint between the given two points 1 Distance 5 units;




7 03 Ellipses And Circles



12 6 Quadric Surfaces Mathematics Libretexts
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Here is the graph of the surface and we've tried to show the region in the \(xy\)plane below the surface Here is a sketch of the region in the \(xy\)plane by itself By setting the two bounding equations equal we can see that they will intersect at \(x = 2\) and \(x = 2\)Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




The Equation X 2 4 Y 2 9 1 Represents The Graph Chegg Com
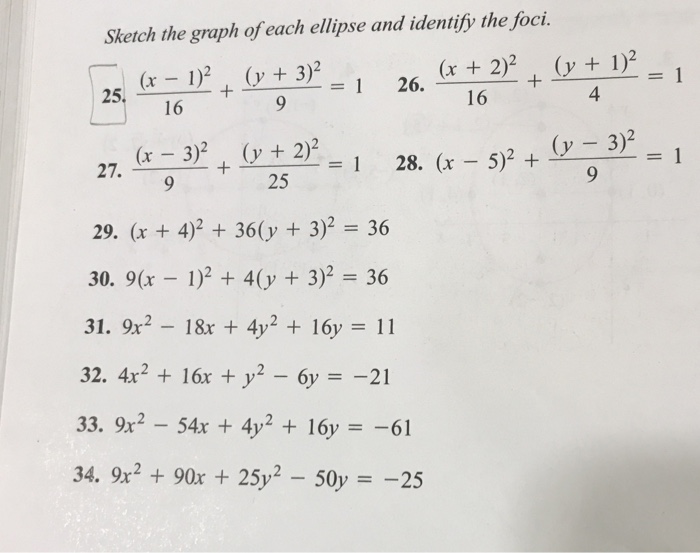



Sketch The Graph Of Each Ellipse And Identify The Chegg Com
Compare and contrast the graphs of the equations x 2 4 y 2 9 = 1 x 2 4 y 2 9 = 1 and x 2 9 y 2 4 = 1 x 2 9 y 2 4 = 1 146 Explain in your own words, the difference between a vertex and a focus of the ellipse Self CheckFind the equations of both tangent lines to the graph of the ellipse {x^2} / 4 {y^2} / 9 = 1 that passes through the point (0, 4) not on the graph View AnswerFollow 81 views (last 30 days) Show older comments Emil Goh on Vote 0 ⋮ Vote 0 Commented Emil Goh on Accepted Answer Joseph Cheng new to matlap



Hyperbola3 Html
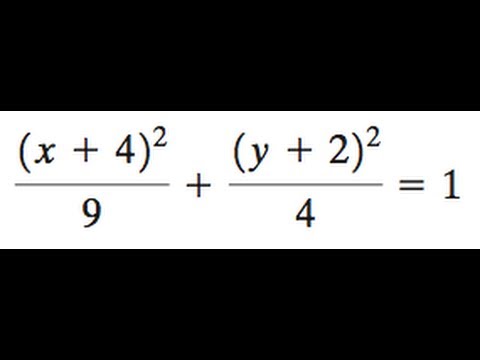



X 4 2 9 Y 2 2 4 1 For The Ellipse Find The Center Foci And Vertices Graph The Equation Youtube
Example of the graph and equation of an ellipse on the The major axis of this ellipse is vertical and is the red segment from (2, 0) to (2, 0) The center of this ellipse is the origin since (0, 0) is the midpoint of the major axis The value of a = 2 and b = 1 The major axis is the segment that contains both foci and has its endpoints onA = 3 Solve for c , c2 = a2 −b2 c2 = 9− 4 > c2 = 5 ⇒ c = ± √5 Use the equation provided above, and "plug it" in Foci (0, − √5);(0,√5)Name Name of 3D surface




Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12
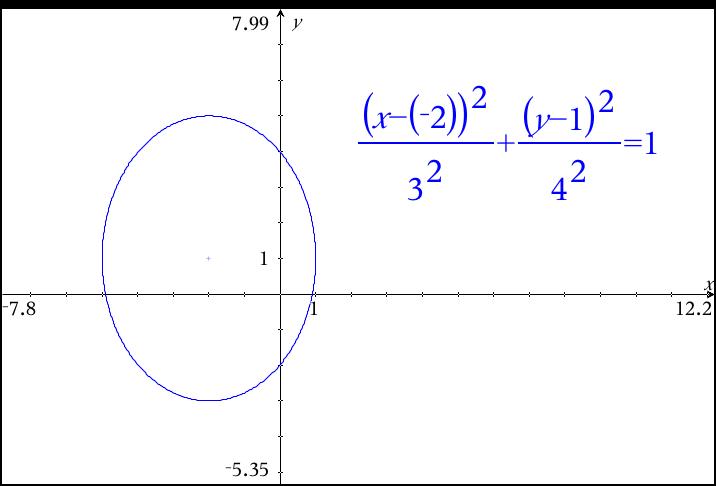



How Do I Graph X 2 2 9 Y 1 2 16 1 Algebraically Socratic
X = y (8 − y) 1, y ≥ 0 and y ≤ 8 View solution steps Steps by Finding Square Root ( x 1 ) ^ { 2 } ( y 4 ) ^ { 2 } = 16 ( x − 1) 2 ( y − 4) 2 = 1 6 Subtract \left (y4\right)^ {2} from both sides of the equation Subtract ( y − 4) 2 from both sides of the equationCompare and contrast the graphs of the equations x 2 4 − y 2 9 = 1 x 2 4 − y 2 9 = 1 and y 2 9 − x 2 4 = 1 y 2 9 − x 2 4 = 1 187 Explain in your own words, how to distinguish the equation of an ellipse with the equation of a hyperbolaQuestion sketch the graph of each ellipse 1x^2/9y^2/4=1 2x^2/9y^2=1 3x^2y^2/4=1 4y^2/4x^2/25=1 5y^2/9X^2/16=1 6x^2/25y^2=1 7x^2y^2/9=1 8x^2y^2/25=1 9x^2/9y^2=1 109x^216y^2=144 119x^225y^2=225 12x^2y^2=1 13y^2x^2=1 Answer by
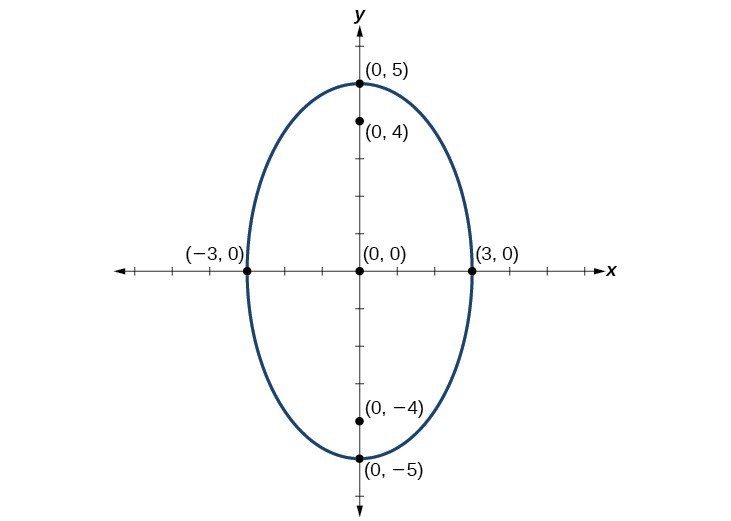



Graphs Of Ellipses College Algebra




Find The Equation Of The Line Through The Points 9 Chegg Com
X 2 4 y 2 9 z 2 = 1 Multiply both sides of the equation by 36, the least common multiple of 4,9 Multiply both sides of the equation by 3 6, the least common multiple of 4, 9 36x^ {2}9y^ {2}4z^ {2}=36 3 6 x 2 9 y 2 4 z 2 = 3 6 Subtract 36x^ {2} from both sides Subtract 3Textbook solution for Calculus Early Transcendental Functions 7th Edition Ron Larson Chapter 101 Problem 5E We have stepbystep solutions for your textbooks written by Bartleby experts!Graph each equation 9) x2 4 y2 9 = 1 x y −8 −6 −4 −2 2 4 6 8 −8 −6 −4 −2 2 4 6 8 10) x2 49 y2 = 1 x y −8 −6 −4 −2 2 4 6 8 −8 −6 −4 −2 2 4 6 ©W U2x0 z1r1 R fK 3uxt rai DSGoUfbtZw va 8rpe Y yLKL SCAq 9 Slwlm ArIi5glh utksj Arue1sFecr 7vVeQd77 u GMZaxdnek xw2iKtlha uI RnLftilnRigt 2e7 XAbl Agle 8b 9rsa
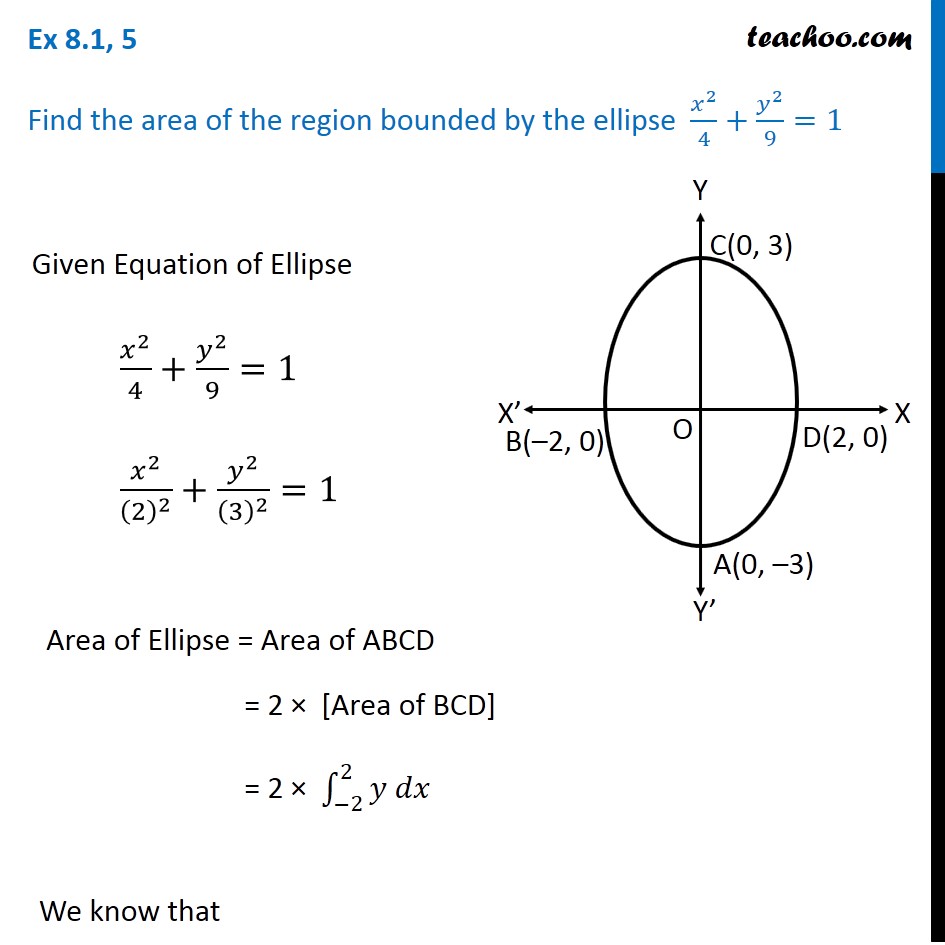



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12




What Is The Graph Of Y 2 16 X 2 9 1 Brainly Com
Find the area of the region bounded by the ellipse x^2/4 y^2/9 = 1 asked in Definite Integrals by Beepin (587k points) application of integrals;Plane z = 1 The trace in the z = 1 plane is the ellipse x2 y2 8 = 1B = 2 a2 = 9;




Vectors And The Geometry Of Space 9 Functions And Surfaces Ppt Download
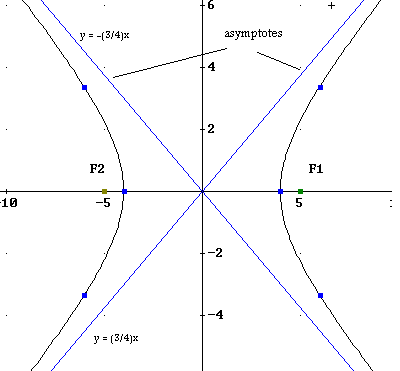



Equation Of Hyperbola Graphing Problems
Graph X 2 Y 2 4 Youtube For more information and source, see on this link https//myoutubecom/watch?v=F2L6YGzWAbM06 Example Evaluate Z 2 0 Z x x2 y2xdydx Solution integral = Z 2 0 Z x x2 y2xdydx Z 2 0 " y3x 3 # y=x y=x2 dx = Z 2 0 x4 3 − x7 3! how to plot ellipse x^2/4y^2/9=1 and circle x^2y^2=1 in a single figure window using ezplot and hold on commands?




X 2 4 Y 2 9 1 Graph Novocom Top
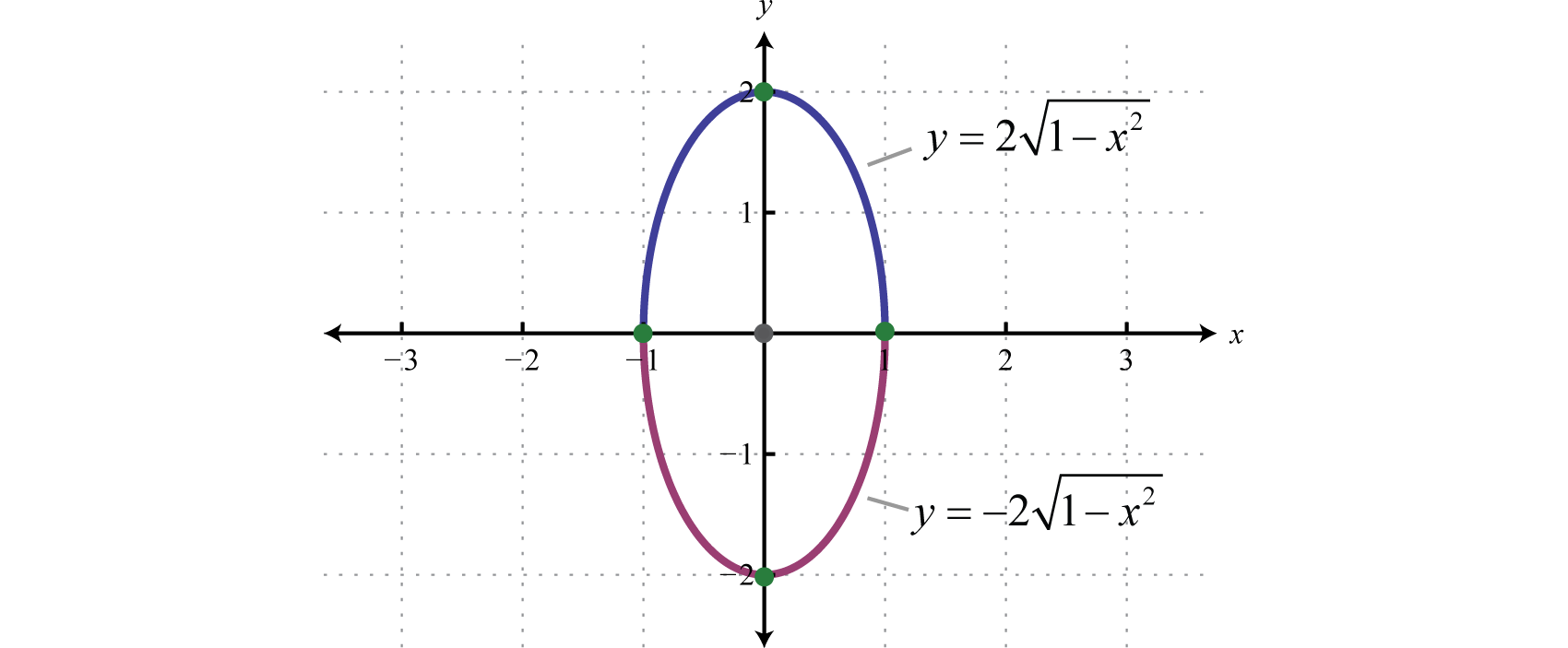



Ellipses
Midpoint ( √ 5 2, − 7 √ 2 2) Determine the area of a circle whose diameter is defined by the given two pointsMatches graph (b) a 3, b 2 0, 0 x 2 4 y 2 9 1 2 Center Horizontal major axis Matches graph (c) a 3, b 2 0, 0 x 9 y 4 1 4 Center Circle of radius 2 Matches graph (f) 0, 0 y2 4 x2 4 1 3 Center Ve rtical major axis Matches graph (d) a 5, b 2 0, 0 x2 4 y2 25 1 5 Center Horizontal major axis Matches graph (a) a 4, b 1 2, 1 (x 22)2 16 Given x2 4 y2 9 = 1 Let's identify the center (0, 0);




7 03 Ellipses And Circles
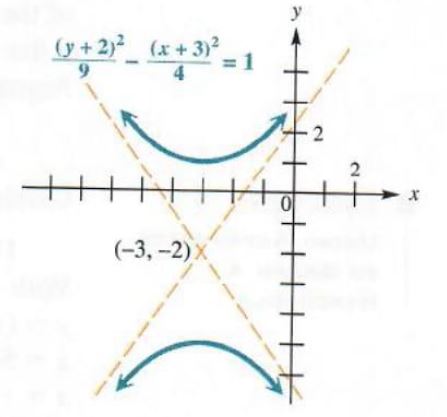



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
Name equation of trace in yzplane ;K = 0 b2 = 4;Sketch the graph of x 2 y 2 = 1 4 9 Solution Check for intercepts If x = 0 then y 2 = 1 which has no solution 9 If y = 0 then x 2 = 1 4 x 2 = 4 so that x = 2 or x =
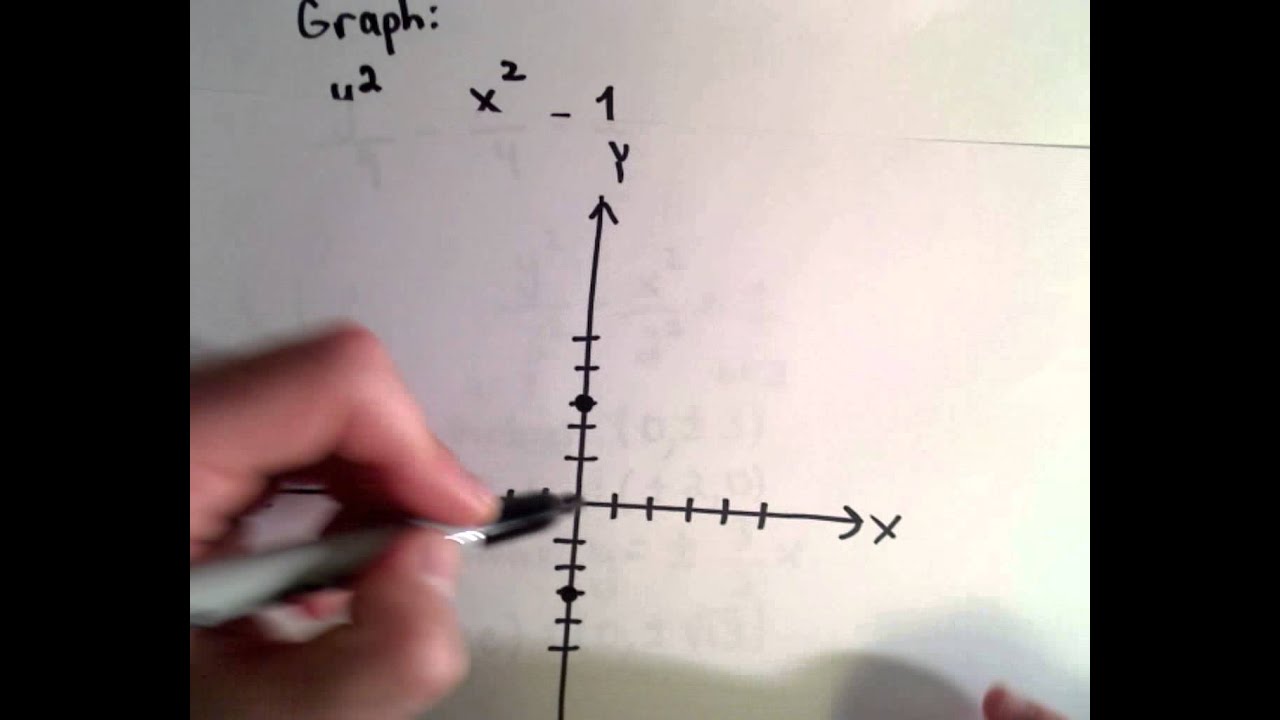



Graphing The Hyperbola Y 2 9 X 2 4 1 Youtube




For The Surface X 2 4 Y 2 9 Z 2 16 1 Give The Chegg Com
Graph the equation x^{2}4 x yy^{2}9=0 Boost your resume with certification as an expert in up to 15 unique STEM subjects this summer This hyperbola will open EastWest and be centered at the origin You will move right and left 2 units from center to find the vertices This comes from sqrt(4) that is the denominator of the x^2 term Then, go up and down 3 units (sqrt(9)) to find corners of a "box" that will create asymptotes for your shape The slopes of the asymptotes will be 3/2 for these reasons(c) Sketch a few traces (choose a few values for k)




Sketch The Graph Of The Following Ellipse X 5 2 4 Y 2 2 9 1 Study Com




Vertices Direction Of A Hyperbola Example 2 Video Khan Academy
Draw a Rough Sketch of the Graph of the Curve X 2 4 Y 2 9 = 1 and Evaluate the Area of the Region Under the Curve and Above the Xaxis CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions 113 Important Solutions 24 Question Bank Solutions ConceptAlgebra Graph (x^2)/4 (y^2)/9=1 x2 4 y2 9 = 1 x 2 4 y 2 9 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 4 y2 9 = 1 x 2 4 y 2 9 = 1Graph (x^2)/4 (y^2)/9=1 x2 4 − y2 9 = 1 x 2 4 y 2 9 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 4 − y2 9 = 1 x 2 4 y 2 9 = 1 This is the form of a hyperbola Use this form to determine the values
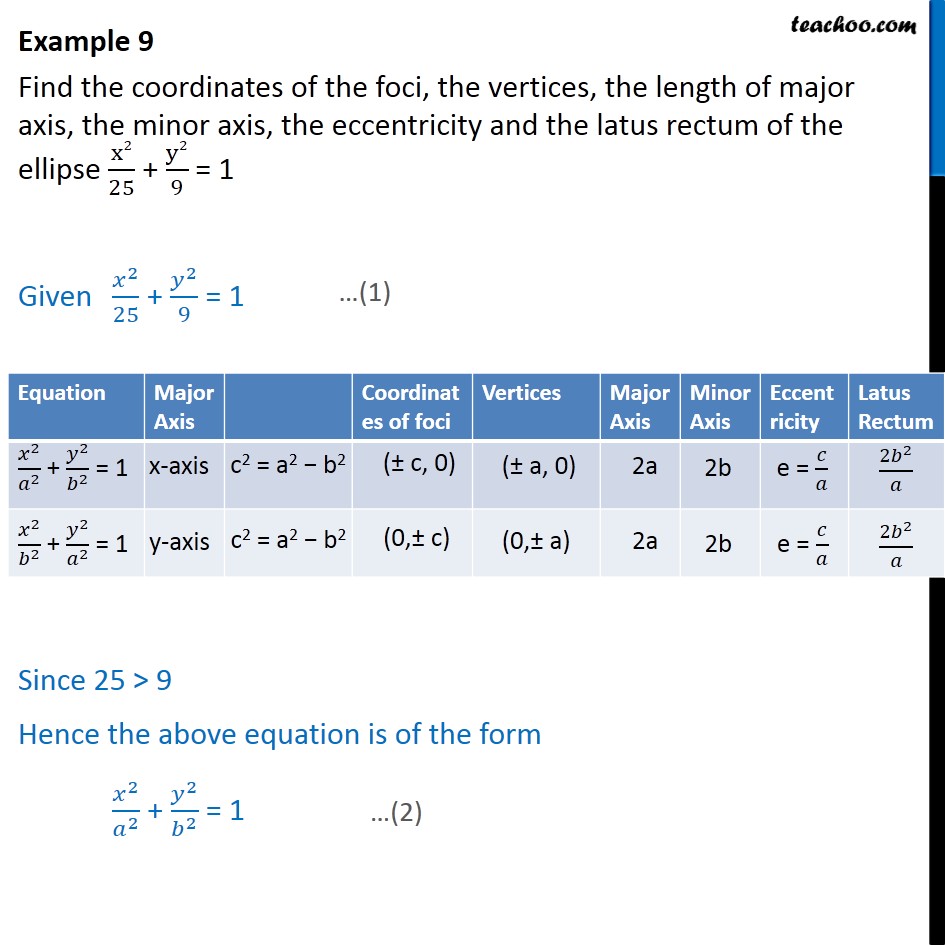



Example 9 X2 25 Y2 9 1 Find Foci Vertices Eccentricity
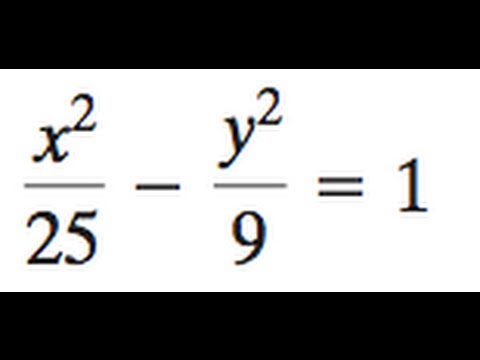



Hyperbola X 2 25 Y 2 9 1 Youtube
249 ELLIPSES Example Find an equation for the ellipse with foci at (4,2) and (4,8) and vertex atAnswer by lwsshak3 () ( Show Source ) You can put this solution on YOUR website!We use implicit differentiation to determine the slope of a line on a given curve Differentiating both sides with respect to x yields math\frac{2x}{4} \frac{2y
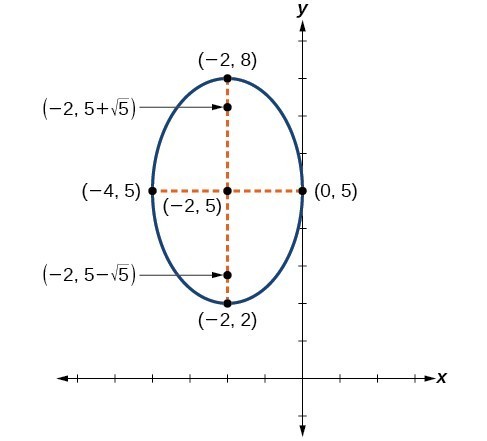



Graphs Of Ellipses College Algebra
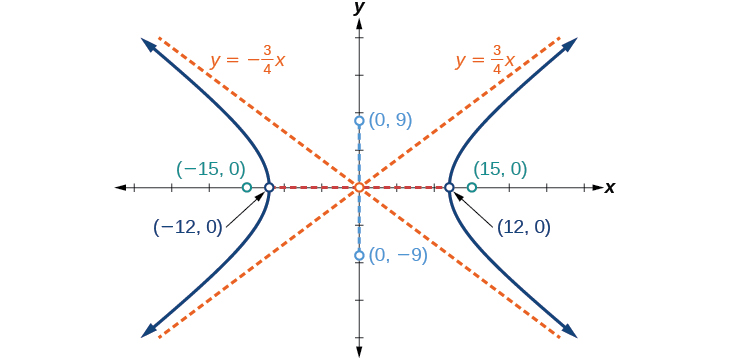



The Hyperbola Precalculus
Graph the ellipse x2 4 y2 9 = 1 Example Graph the ellipse (x3)2 4 (y1)2 9 = 1 What are the center, vertices, and foci? how to plot ellipse x^2/4y^2/9=1 and circle x^2y^2=1 in a single figure window using ezplot and hold on commands?(b) What kind of trace do we get (what is the name of the graph of the trace)?



1
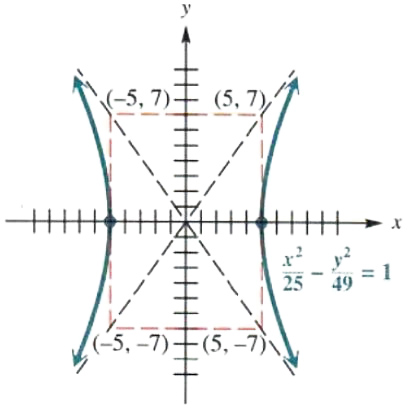



Solve Ellipse And Hyperbola Step By Step Math Problem Solver
1 72 Finding Volume Using Cross Sections Warm Up Find the area of the following figures 1 A square with sides of length x 2 A square with diagonals of length xMidpoint ( − 2, 1 2) 3 Distance 4 √ 10 units;In Figure 1118 (a), we show part of the graph of the equation x 2 y 2 = 1 by sketching 3 circles the bottom one has a constant zvalue of 15, the middle one has a zvalue of 0 and the top circle has a zvalue of 1 x 2 4 y 2 9 = 1 24 y = 1 x In Exercises 25




Graphing Hyperbola With The Equation X 2 9 Y 2 4 1 Youtube




Write The Equation Of The Ellipse Shown In The Graph A X 1 2 4 Y 2 2 9 1b X 1 2 9 Brainly Com




Algebra 2 Ch 9 Solutions Key Ch 9 Solutions Key Pdf Peninsula



How To Construct The Graph Of X 2 Y 2 9 Quora




Vertices Direction Of A Hyperbola Example 2 Video Khan Academy




Sketch The Surface X 2 4 Y 2 9 Z 2 1 Find The Chegg Com




Solving Systems By Graphing
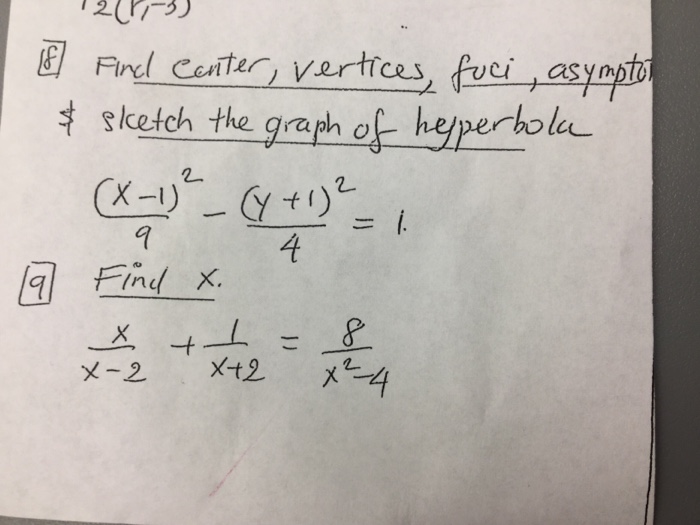



Find Vertices Sletch The Graph Of Chegg Com




Mrs Rivas Ppt Download



14 1 Conic Sections Graphing Calculator By Mathlab User Manual




Find The Eccentricity Of The Ellipse X 2 2 4 Chegg Com
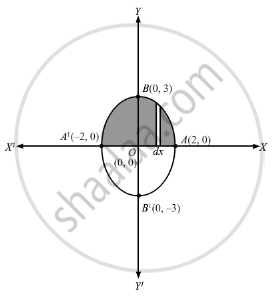



Draw A Rough Sketch Of The Graph Of The Curve X 2 4 Y 2 9 1 And Evaluate The Area Of The Region Under The Curve And Above The X Axis Mathematics Shaalaa Com



1




Identifying Linear Functions Warm Up Lesson Presentation Lesson



Graphing A Circle Help Mathskey Com



1




Find The Vertices And Foci Of Each Ellipse X 2 64 Chegg Com
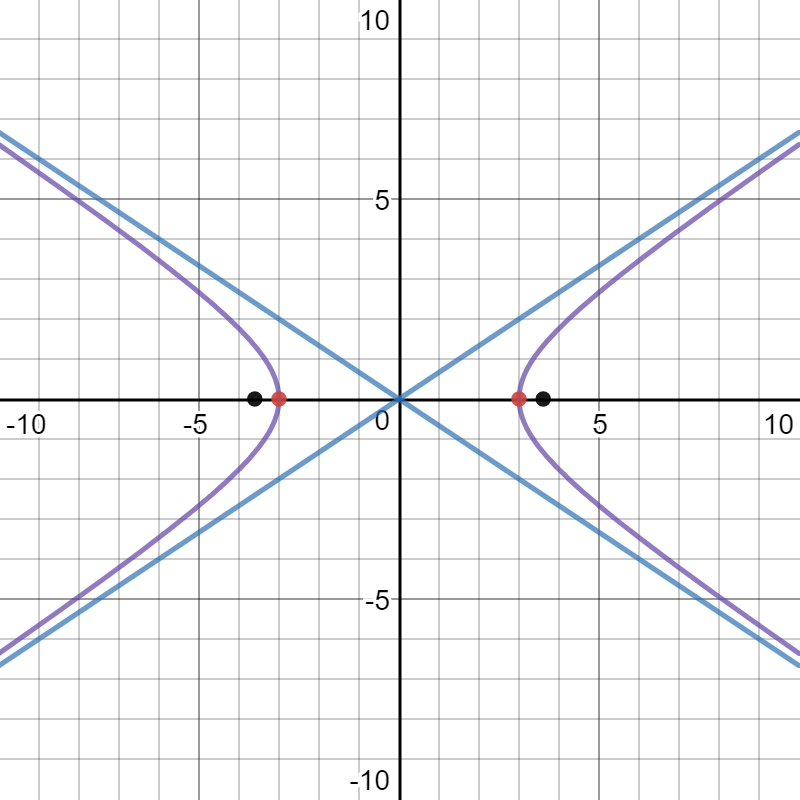



How Do You Find The Foci And Sketch The Hyperbola X 2 9 Y 2 4 1 Socratic




Circles



Ellipses And Hyperbolae



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora
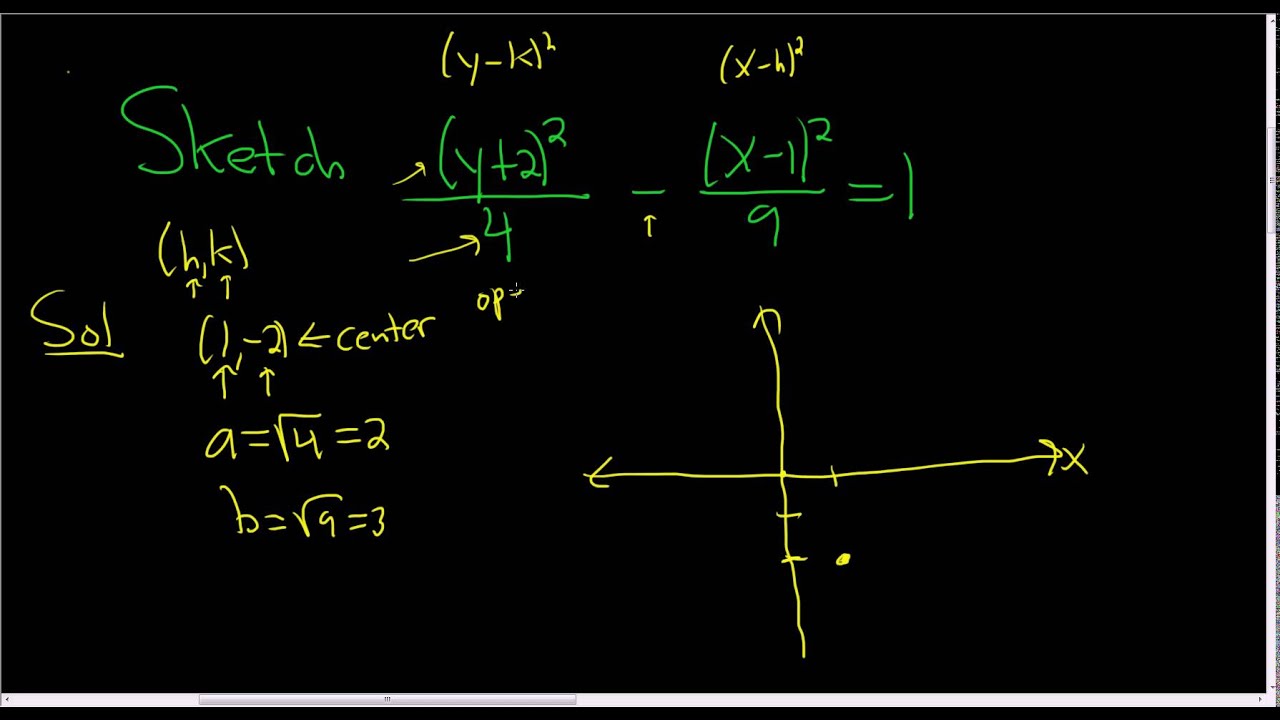



Graph The Hyperbola Y 2 2 4 X 1 2 9 1 Youtube




The Ellipsoid Shown At Right Has Equation X 2 9 Chegg Com



Solution Graph X 3 2 Y 1 2 4 Y 2 2 4 4 1 X 1 X 2 2 9 Y 3 2 4 1 X 2 2 4 Y 3 2 9 1 Thanks Soo Much




X 2 4 Y 2 9 1 Graph Novocom Top



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora
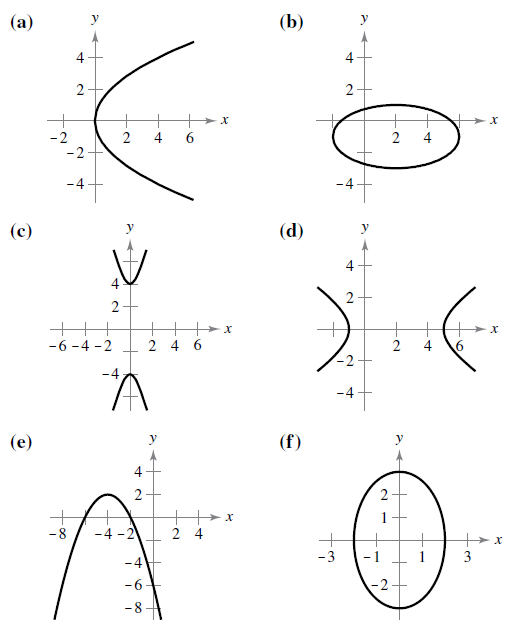



Matching In Exercises 5 10 Match The Equation With Its Graph The Graphs Are Labeled A B C D E And F X 2 4 Y 2 9 1 Bartleby




Which Is The Graph Of X 2 9 Y 2 16 1 Brainly Com



Quiz Chapter 10



Green Globs And Graphing Equations Buffalo State College Flip Ebook Pages 1 6 Anyflip Anyflip




Rectangular Coordinate System
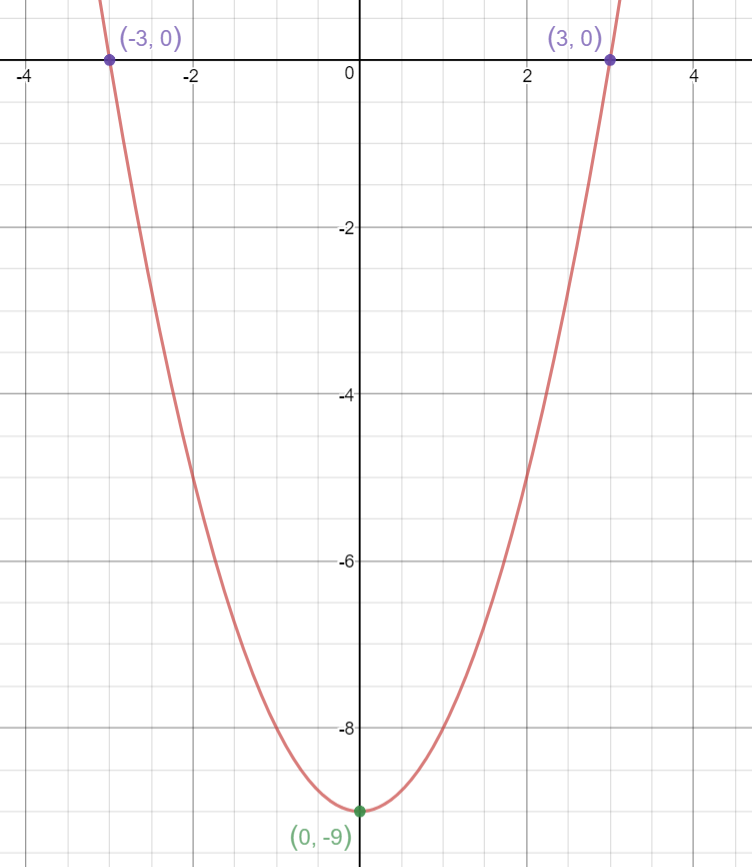



How Do You Graph Y X 2 9 Socratic



Solution 1 X 1 2 9 Y 3 2 4 1 What Is The Center Vertices Foci And Co Vertices In Short Give The Conic Section
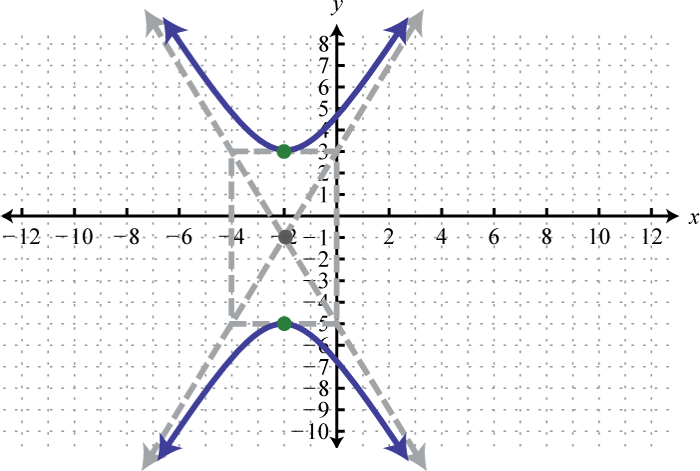



Hyperbolas




Match The Equation With Its Graph The Graphs Are Chegg Com



Ellipses And Hyperbolae



Solution Graph X 3 2 Y 1 2 4 Y 2 2 4 4 1 X 1 X 2 2 9 Y 3 2 4 1 X 2 2 4 Y 3 2 9 1 Thanks Soo Much
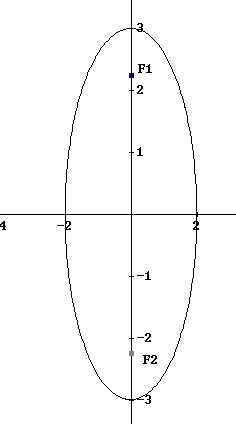



Equation Of Ellipse Problems




X 2 2 4 Y 3 2 9 1 Hyperbola Youtube




Section 7 3 The Ellipse Ellipse A Set Of Points In A Plane Whose Distances From Two Fixed Points Is A Constant Ppt Download




Ex 11 4 1 Find Foci Vertices Of Hyperbola X 2 16 Y 2 9 1



1
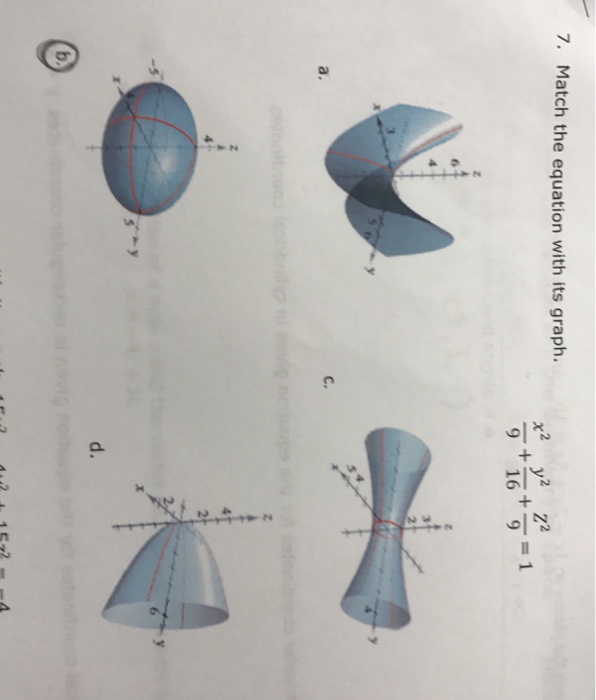



Match The Equation With Its Graph X 2 9 Y 2 16 Chegg Com




How Do You Graph X 2 Y 2 4 Socratic



Find The Foci Of The Graph Of X 2 4 Y 2 9 1 Mathskey Com




Which Graph Represents The Hyperbola Y 2 6 2 X 2 2 2 1 Brainly Com



Http Www Jessamine K12 Ky Us Userfiles 1044 Classes Key to practice test unit 6 conic sections Pdf Id 329
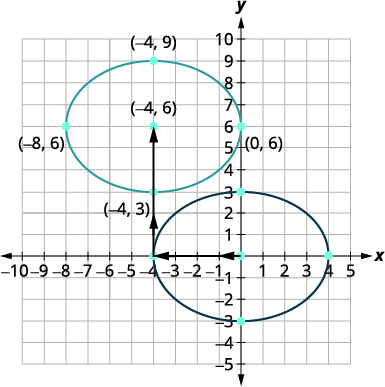



11 4 Ellipses Mathematics Libretexts
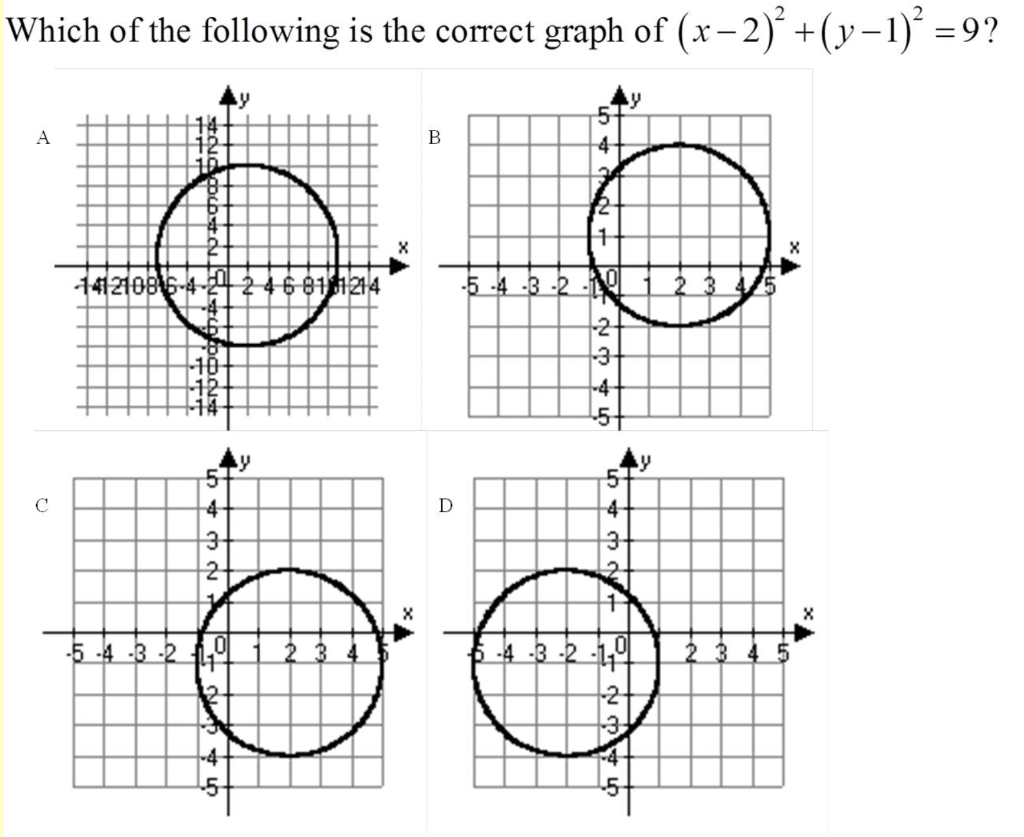



Which Of The Following Is The Correct Graph Of X 2 Chegg Com



Hyperbola3 Html
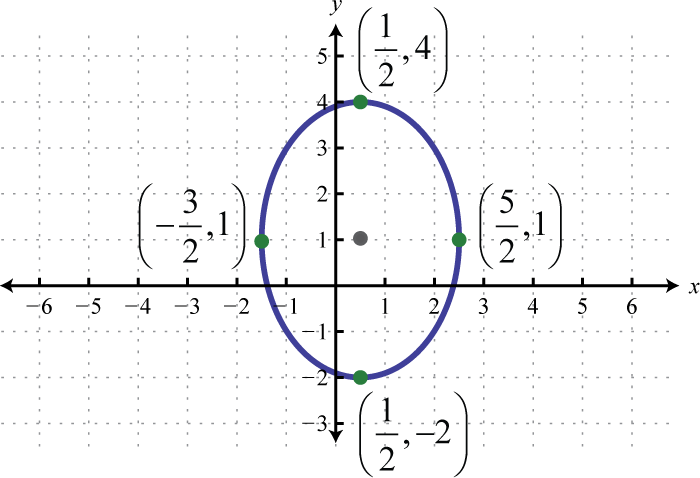



Ellipses
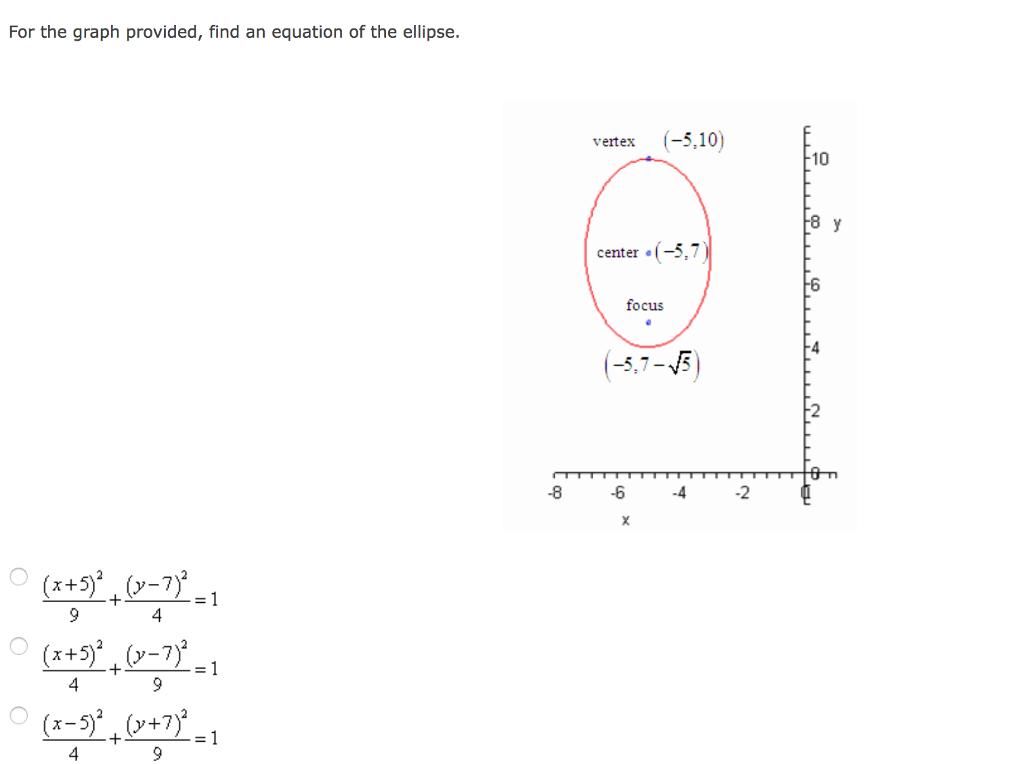



Solved For The Graph Provided Find An Equation Of The El Chegg Com



12 6 Quadric Surfaces Mathematics Libretexts




Example 1 Graph The Equation Of A Translated Circle Graph X 2 2 Y 3 2 9 Solution Step 1 Compare The Given Equation To The Standard Form Of Ppt Download
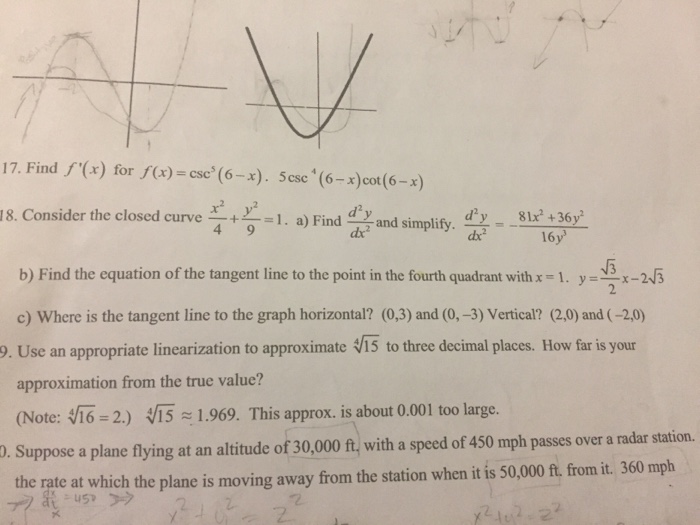



Solved Consider The Closed Curve X 2 4 Y 2 9 1 A Find D Chegg Com




Graph X 4 2 4 Y 2 9 1 Brainly Com




Graph The Hyperbola With Equation X 1 2 9 Y 4 2 25 1 Brainly Com
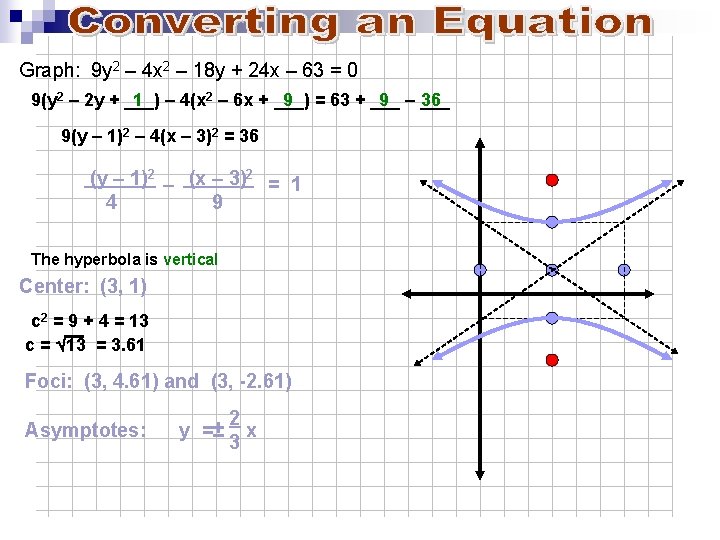



Conic Sections 11 1 Parabola Conic Sections Parabola



Ellipses And Hyperbolae



Pslv Egs Circles




7 04 Hyperbolas
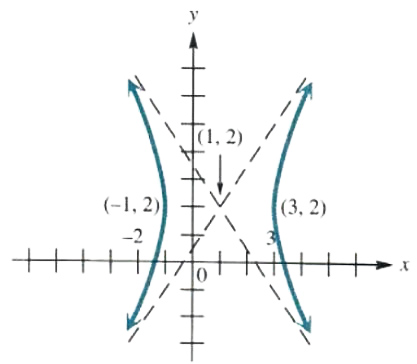



Solve Ellipse And Hyperbola Step By Step Math Problem Solver




Graph X 2 Y 2 4 Youtube
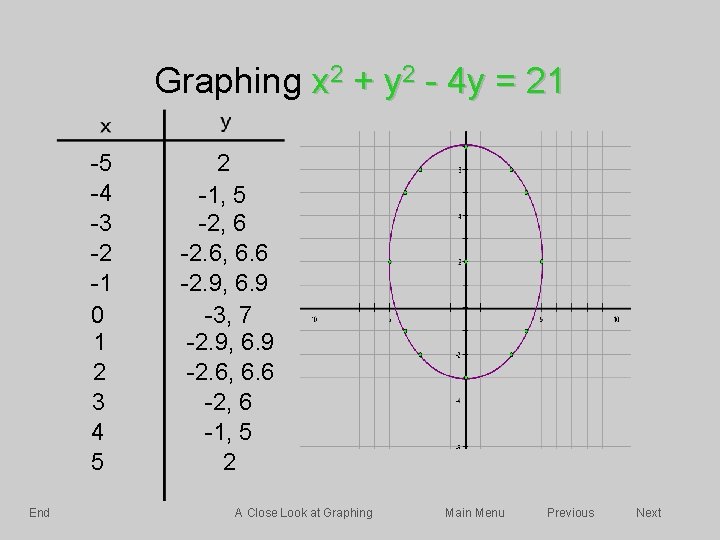



Skip Introduction A Closer Look At Graphing The
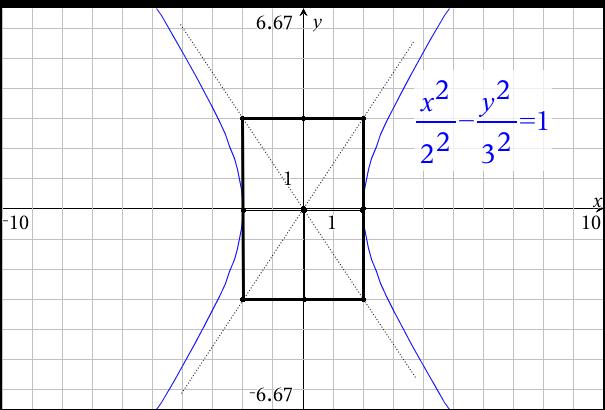



How Do You Graph X 2 4 Y 2 9 1 Socratic



The Smaller Region Bounded By The Ellipse X 2 16 Y 2 9 1 And A Straight Line 3x 4y 12 What Should Be The Area Of That Smaller Region Quora




7 04 Hyperbolas




Graph The Hyperbola X 1 2 4 Y 2 2 9 1 Youtube



0 件のコメント:
コメントを投稿