Solve the following linear equation systems using the elimination method A (4x3y = 9 3x 2y = 11)} B {(X2y = 5 X 2y = 3} C {(2x7y = 1214y 4x = 12)} Best Answer 3x4y=11 5x2y=5 note that, if we multiply the second equation by 2 and add it to the first one, we can "eliminate" y So we have2nd Substitution Method 3rd Elimination Method ⬜ Substitution Method At least one of the two equations are y= or x= 1 "Substitute" that expression into the other equation and solve for the missing variable 2 Use the first variable answer you found and plug into either original equation to find the second missing variable 3

Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2
X+y/2=4 x/3+2y=5 by elimination method
X+y/2=4 x/3+2y=5 by elimination method-STATE 0 Write down the system as given x y z = −2 2 x − 3 y 4 z = 14 5 x 2 y − 3 z = 10 STATE 1 Express z in terms of x and y x y z = −2 2 x − 3 y 4 (−2 − x − y) = 14 5 x 2 y − 3 (−2 − x − y) = 10 STATE 2 Simplify the equat Solve the following system of equations by elimination method x y = 7xy;




Solve X Y 7 And 3x 2y 11
Solve the Given equation in Elimination method and Substitution MethodSolve the system 3xy=8 and x2y=5 by the elimination method 3xy=8 x2y=5 6x2y=16 Multiplying each term on both sides of the equation by 2 x2y=5 7x = 21 x = 3 solving for y 3x y = 8 98 = y 1 = y Pt(3,1) is the solution for this sytemGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Substitution 1 2 From eq 2, Substitute into eq 1,Elimination method x2y=2x5, xy=3 \square!First, you have to equate the coefficients of the y so equation 1 will be doubled 4x 2y = 0 x 2y = 5
Given XXXx −2y = 5 XXX2x − 3y = 10 Rewriting as augmented matrix XXX1 −2 5 2 −3 10XXX1 2 Subtracting 2 times the first row from the second row XXX1 −2 5 0 1 0XXX1 3 = 2 −2 × 1 Adding 2 times row 3 to the first row XXX1 0 5 0 1 0XXX4 3 = 1 2 × 3Steps for Solving Linear Equation 5x2y= − 5 x 2 y = 2 0 Add 5x to both sides Add 5 x to both sides 2y=5x 2 y = 2 0 5 x The equation isSolve the following systems of equations x y/2 =4 x/3 2y =5 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
Graph y=2(x3)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus Tap for more stepsSelina solutions for Concise Mathematics Class 9 ICSE chapter 6 (Simultaneous (Linear) Equations (Including Problems)) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear yourThere Are Actually 4 methods of solving this We have, 2x 3y = 11(i) and, 5x 2y = 18(ii) i) Elimination Method First choose which variable you want to eliminate I'm going with y So, Multiply the eq(i) with 2 first It will turn into, 4x 6y = 22(iii) Now, Multiply the eq(ii) with 3




1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y



If X Y 3 X Y 1 Then What Is X Y Quora
The equation is in standard form 2x=5y4 2 x = 5 y − 4 Divide both sides by 2 Divide both sides by 2 \frac {2x} {2}=\frac {5y4} {2} 2 2 x = 2 5 y − 4 Dividing by 2 undoes the multiplication by 2 Dividing by 2 undoes the multiplication by 2 x = 1 y = 2 Ok So prefer the elimination method, but you can do this with substitution as well First put the equations on top of each other x 2y= 5 2x3y=4 Then find the variable that would be easiest to cancel out I think it's x because you only have to modify one of the equations Let's multiply the first equation by 2 This will allow us to cancel out the two x's in the5x2y=3,x5y=4 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 5x2y=3 Choose one of the equations and solve it for x by isolating x




X Y 2 4 X 3 2y 5 Plz Solve This By Elimination Method Brainly In



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora
Question 1 Solve the following systems of linear equations by Gaussian elimination method 2x − 2y 3z = 2, x 2y − z = 3, 3x − y 2z = 15x2y=5 #" "# (2)Click here👆to get an answer to your question ️ Solve the following pair of linear equations by the elimination method and the substitution method x2 2y3 = 1 and x y3 = 3




Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables




Please Help Me Answering The Following Problems 18 Chegg Com
2x – 3y = – xy asked in Linear Equations by Anika01 ( 571k points) pair x 2y 5 3x 2 3y 10 solve by elimination method Mathematics TopperLearningcom dzs9yv22 Starting early can help you score better!\\begin{aligned}&x2y=10\\&2xy=5\end{aligned}\ > <




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6




Class 10 Linear Equations In Two Variables 1 2 X 2y 5 3 3x 2y 3 2 And 5 4 X 2y Youtube
Solve {eq}2 x 3 y = 14 {/eq} and {eq}3 x 4 y = 4 {/eq} by the method of elimination Elimination Method Definition Elimination method is used to solve the linear equation in two variables x = 4, y = 1 WARNING!The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically




Solving A System Of Equations Using A Matrix Precalculus Socratic




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
Solve by elimination method,xy/2=4,x/32y=5 Answer Stepbystep explanation The given equations are and which can be rewritten as (1)High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables In this blog post,Multiply the both sides of the first equation by 2 Distribute and multiply Now add the equations together You can do this by simply adding the two left sides and the two right sides separately like this Group like terms
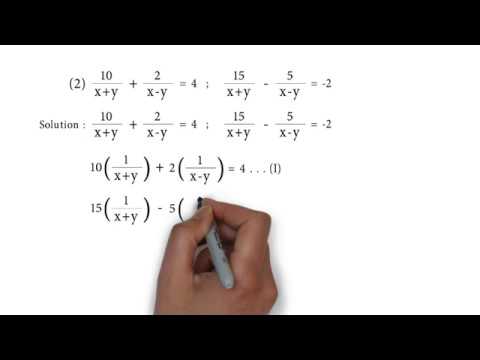



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube




Solve The Following Pair Of Linear Equations By The Elimination M
(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3 Transcript Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 y = 2 x = 1 We can solve this one of two ways;




Solving Linear Systems



Canvas Bham Ac Uk Courses Files Download Verifier Olsyulszmw31bkuumjmm1h3moiw4myavdszsni9s Wrap 1
Question Solve the question by the method of elimination by substitution Question 3x4y= x2y=5 Answer by Fombitz() (Show Source) You can put this solution on YOUR website!Solving Linear Equations by Elimination Method Here we are going to see some example problems of solving linear equations in two variables using elimination method The various steps involved in the technique are given below Step 1 Multiply one or both of the equations by a suitable number (s) so that either the coefficients of firstThis is basic linear algebra Solve a system of two linear equations in two unknowns (variables) Use the (GaussJordan) elimination method to eliminate one variable linear system 1 math x 2y = 5/math 2 math3x y = 1/math Eliminate
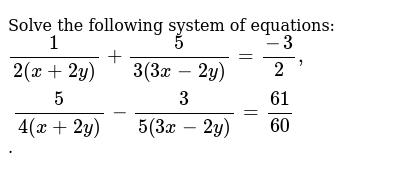



Solve The Following System Of Equations 1 2 X 2y 5 3 3x 2




3 Systems Of Linear Equations
Question Need help solving system by elimination method x/2 y/3 = 7/6 2x/3 3y/4 = 5/4 Thank you Found 3 solutions by Alan3354, Fombitz, rothauserc The Questions and Answers of 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two min From substitution, elimination,and cross multiplication method?How to Solve a System of Equations by Elimination from Chapter 29 / Lesson 5 77K After watching this video lesson, you will have learned how to solve a system of equations by using the




Graph Graph Inequalities With Step By Step Math Problem Solver



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community
Click here👆to get an answer to your question ️ Solve by elimination method x y = 5 2x 3y = 4 Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables Solve the following pairs of linear (simultaneous) equation by the method of elimination by substitution 2 x 3 y = 8, x – y = – 2 (4) Adding equation (3) and (4) x – y = – 2 x y = 6 2x = 4 x = 2 From (3) 2 y = 6 y = 4 Question 10 For solving pair of equation, in this exercise use the method of elimination by equating coefficients 41x 53y = 135 53x 41y = 147 AnswerChoose one of the equations and solve it for x by isolating x on the left hand side of the equal sign x\left (k\right)y=2 x ( − k) y = 2 Add ky to both sides of the equation Add k y to both sides of the equation x=ky2 x = k y 2 Substitute ky2 for x in the other equation, 3x2y5=0



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




Write The Augmented Matrix For Each System Do Not Chegg Com
Steps for Solving Linear Equation x = 2 y 5 x = 2 y − 5 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2y5=x 2 y − 5 = x Add 5 to both sides Add 5 to both sidesOr click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding orSOLUTION Use elimination method in solving this;tnx x3y=5 2xy=5 You can put this solution on YOUR website!



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




22 4 3x 6 317 3 2x 3y 11 4 X 2y 8 6 26 Chegg Com
Avail 25% off on study packSteps for Solving Linear Equation x2y=5 x 2 y = 5 Subtract x from both sides Subtract x from both sides 2y=5x 2 y = 5 − x Divide both sides by 2 Divide both sides by 2 Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label the equations Label the equations A and B (A) 3x 2y = 4 (B) x 4y = 3 Step 2 Isolate one of the variables To use the substitution method, we need to isolate one of the variables We will isolate variable x in equation B in this example x




How Do You Solve X 1 2 Y 2 3 4 And X 2y 5 Socratic




Solving A System Of Equations Using A Matrix Precalculus Socratic
Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y You can use the "elimination" method to solve the equation system To do this, you must destroy one of two variables (x, y) You have to equalize the coefficients in both equations by choosing one of the variables 'x' or 'y' x3y=2 #" "# (1) ;Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!




Solve 2x Y 5 And 3x 2y 8




Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2
By elimination or by substitution I don't know which one is your preferred method so I will do both Both methods will yield the same answer Method 1 Elimination 2xy =0 x 2y = 5 Let us use x as the variable we want to work out;Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10Solve the Following Systems of Equations `X Y/2 = 4` `X/3 2y = 5`




X Y 6 X Y 2 By Elimination Method Novocom Top




0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question
Solve by Addition/Elimination 3x2y=16 2x2y=4 3x 2y = 16 3 x 2 y = 16 2x − 2y = 4 2 x 2 y = 4 Add the two equations together to eliminate y y from the system




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




X Y 5 2x 2y 10 Elimination Method Novocom Top



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community



If X Y 3 X Y 1 Then What Is X Y Quora




7 Solve The Following System Of Linear Equations Chegg Com



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Revision 1 Simultaneous Linear Equations In Two Unknowns A Pair




Solve Graphically The System Of Equations X Y 3 3x 2y 4 Mathematics Topperlearning Com Ja91bwemm




The Solution Of 2x Y Z 1 X 2y 3z 1 3x 2y 4z 5 Is 1 1 2 3 2 1 2 3 3 1 3 2 4 Youtube




J19




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Solving Simultaneous Equations Equations And Inequalities Siyavula




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6




Solve Equations Using Substitution Method 2x Y 3 And 4x Y 3




Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy



The Substitution Method



Q Tbn And9gcrgcc3fezv8atx4b2tvoeaa3ipgkmqphkf Ft0ik F D5v3h0cr Usqp Cau




Solved 8 Solve The Linear System Of Equations 2 X Y 1 U Chegg Com




X Y 6 X Y 2 By Elimination Method Novocom Top




Solve The Simultaneous Equations 10 X Y 2 X Y 4 15




Elimination Method Day 1 Ppt Download




10 X Y 2 X Y 4 15 X Y 9 X Y 2 By Substitution Method Brainly In




Elimination Method Day 1 Ppt Download




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top



Solve The Following Systems Of Equations 2 X 3 Y 2 4 X 9 Y 1 Sarthaks Econnect Largest Online Education Community



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic



Is The Gauss Elimination Method X 2y 3z 1 2x 3y 8z 2 X Y Z 3 Quora
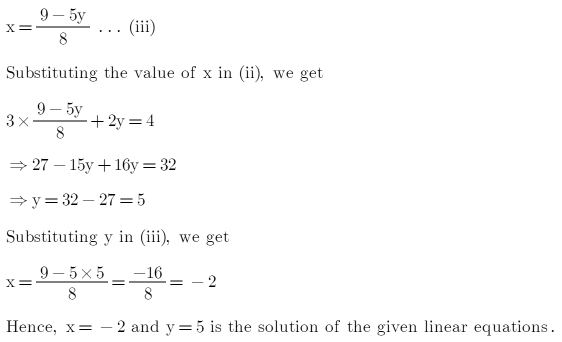



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll



2



Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf



Mfm2p




X Y 2 4 X 3 2y 5 Solve It By Elimination Method Brainly In




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr




Solve 3x 2y 11 And 2x 3y 4




4 3 Systems Of Linear Equations In Three Variables
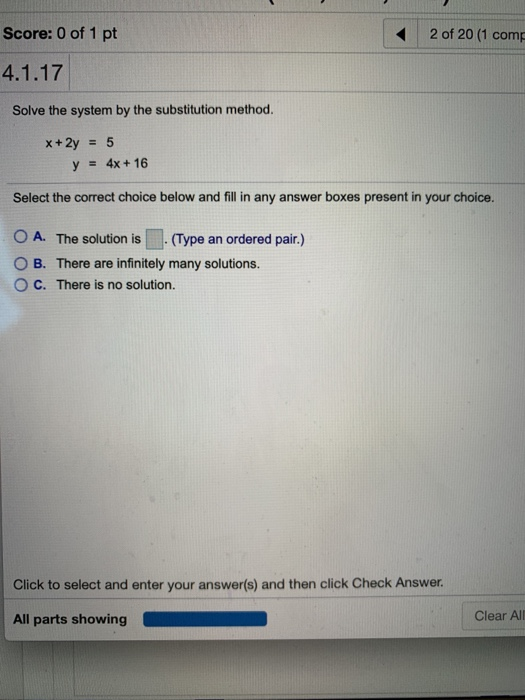



Score 0 Of 1 Pt 2 Of 1 Comp 4 1 17 Solve The Chegg Com




Need With Help Understanding Gauss Elimination In A Simple Way 3x 2 7x 3 4 X 1 Homeworklib



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community



How Do You Solve X 2y 6 And X Y 2 Socratic




Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations
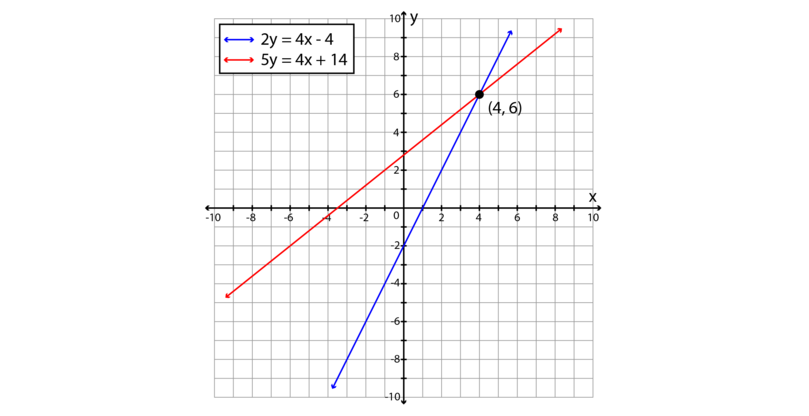



Elimination Method Simultaneous Linear Equations Siyavula




Hw 3 Due 9 27 Solve Each System Of Equations Chegg Com



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community




For Solving Each Pair Of Equations In This Exercise Use The Method Of Elimination By Equating Coefficients Begin Array L 7 Sqrt 3 2 Y 9 X Text 2 3 X Y 23 Frac X 3 Frac Y 4 4 End Array




Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube




Ex 3 4qno1 1 Solve X Y 5 2x 3y 4 By The Elimination Method Youtube




7 Solve The Following System Of Linear Equations Chegg Com




Answers




Algebra



Search Q 3x Y 2b7 11 2b2 3d10 And 2y 2bx 2b11 7 3d10 By Elimination Method Tbm Isch




Asap Please 1 Solve The Following Simultaneous Equations 1 Graphically And Ii Using The Elimination Method Homeworklib




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



The Elimination Method




7 Y 3 2 X 2 14 4 Y 2 4 X 3 44 Solve Equation Using Elimination Method Brainly In




Solve X Y 7 And 3x 2y 11




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




Solve X 2 Y 5 4 And X 7 Y 15 3 By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com



Simultaneous Equations Gmat Math Study Guide




Solved X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Brainly In



Systems Of Linear Equations



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection




X Y 5 2x 2y 10 Elimination Method Novocom Top




Solve By Elimination Method X Y 2 4 X 3 2y 5 Brainly In




100以上 Solve By Substitution Method X Y 14 X Y 4 Solve By Substitution Method X Y 14 X Y 4




X Y 6 X Y 2 By Elimination Method Novocom Top



Find The Circumcenter Whose Sides Are 3x Y 5 0 X 2y 4 0 5x 3y 1 0 Quora




Solved By Elimination Method 2x Y 5 And 3x 2y 8 Brainly In




Solving A System Of Equations Using A Matrix Precalculus Socratic




Ch 3 5 Elimination Multiplication Ppt Download




If The Equation Kx 2y 5 3x Y 1 Has No Solution Then What Is The Value Of K Quora



0 件のコメント:
コメントを投稿